El prodigioso número de oro y la divina proporción

Al escribir sobre la exigencia de presentar una fotocopia de la cédula “ampliada al 150%”, mencioné que la cédula de ciudadanía colombiana tiene un tamaño igual al de las tarjetas de crédito y que esa medida universal no es un capricho, pues la relación entre la longitud de sus lados esconde un número secreto extraordinario (ver https://blogs.elespectador.com/actualidad/ecuaciones-de-opinion/la-cedula-ampliada-al-150)

Nos hemos familiarizado desde niños con los números enteros positivos principalmente y en muchos casos ha resultado difícil posteriormente dominar los negativos y por supuesto el cero. Aun cuando también nos hemos acostumbrado al uso de los números enteros en un sistema decimal por la aparente comodidad que éste nos ofrece para las operaciones aritméticas cotidianas y aun cuando también hemos trasladado a nuestras unidades de medida estos usos, logrando casi una uniformidad global de la que solo se apartan algunas medidas tales como las que aún se expresan en galones, docenas, millas, pulgadas, fanegadas, yardas, arrobas, onzas; y aun cuando solo sobreviven algunas pocas divisiones que no son decimales, tales como los minutos de las horas, los días de la semana, los meses del año o algunas escalas de medición no métrica decimal, la verdad es que la naturaleza, no solo no se puede medir ni comprender con el uso de los números enteros únicamente, sino que tampoco es posible hacerlo con la sola inclusión de las fracciones.

Con más frecuencia de lo que podemos creer, en la naturaleza, en la cotidianidad, aparecen cantidades que ya los griegos habían denominado inconmensurables porque no son decimales periódicos, como los que provienen de las fracciones entre enteros. Me refiero a los llamados números irracionales que también conforman un subconjunto infinito de números reales. Algunos se han vuelto famosos porque los hemos tenido que aprender desde la escuela; tal es el caso de π, e o √2. Pero conocemos mucho menos un importante número que se ha bautizado como φ y que no goza de tanta popularidad.

El número φ es conocido como el número de oro, por cuanto es una perfecta medida para muchas cosas presentes en la naturaleza y para otras que utilizamos diariamente. Este número, con infinitas cifras decimales, surge de la división de un segmento en dos partes a y b, guardando las siguientes proporciones: la longitud total (a+b) es a la longitud del más largo a, como la longitud de a es al más corto b. 

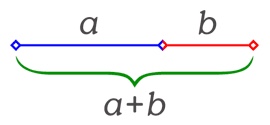
De esta proporción a/b surge el valor de φ, como la solución positiva de una ecuación de segundo grado:

(a+b)/a = (a/b), entonces:

1 + (b/a) = (a/b) =: φ

1 + 1/φ = φ

φ² – φ – 1 = 0

por lo tanto

φ = (1+√5)/2.

Expresado en forma decimal, con algunas de sus infinitas cifras,

φ ≈ 1,6180339887498948… . 

De acuerdo con algunos historiadores hay constancia de haberse conocido el número de oro φ en civilizaciones antiguas como la babilónica, hacia el año 2000 a. C., pero la referencia más divulgada se origina en el dibujo que Leonardo Da Vinci hizo hace 500 años para ilustrar el libro ‘La Divina Proporción‘ del matemático Luca Pacioli, proponiendo una figura humana masculina perfecta (homo quadratus). 

En el dibujo de Da Vinci las distintas partes del cuerpo guardan una proporción áurea. En efecto, “El Hombre de Vitruvio”, como se le conoce en honor a Marco Vitruvio, un destacado arquitecto romano del siglo I a. C., quien publicó un tratado de arquitectura, escrito entre el 27 y el 23 a. C. fue pintado atendiendo la mención que hacía Vitruvio de las proporciones que consideraba “ideales” para la figura humana: “… El ombligo es el punto central natural del cuerpo humano, ya que si un hombre se echa sobre la espalda, con las manos y los pies extendidos, y coloca la punta de un compás en su ombligo, los dedos de las manos y los de los pies tocarán la circunferencia del círculo que así trazamos. Y de la misma forma que el cuerpo humano nos da un círculo que lo rodea, también podemos hallar un cuadrado donde igualmente esté encerrado el cuerpo humano. Porque si medimos la distancia desde las plantas de los pies hasta la punta de la cabeza y luego aplicamos esta misma medida a los brazos extendidos, encontraremos que la anchura es igual a la longitud, como en el caso de las superficies planas que son perfectamente cuadradas.”

Inspirado en esta descripción, Leonardo da Vinci se dispuso a hacer su propia versión de aquel humano idealizado de Vitruvio. Y esto fue lo que obtuvo:

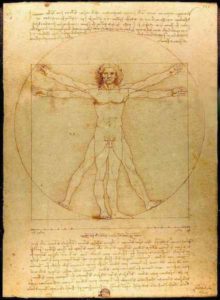
si se divide la altura total de un hombre entre la altura de su ombligo, nos da como resultado el número de oro. Igualmente, el cociente entre la altura del hombre y la distancia del ombligo a la punta de las manos con los brazos extendidos es también el número áureo. (Puede usted, apreciado lector, hacer ahora esa prueba con su propio cuerpo).

Algunos de ustedes se sorprenderían de descubrir la infinidad de medidas en las que está presente esta proporción, el listado escapa a la intención de este texto, no obstante quiero compartirles algunos objetos rectangulares que usamos a diario y que han sido diseñados conservando la proporción áurea que se obtiene dividiendo sus dimensiones de largo y ancho: las tarjetas de crédito, la licencia de conducción, la cédula de ciudadanía, las hojas de papel tamaño oficio, ventanas, muebles y hasta las cajetillas de cigarrillos.

Hay una famosa sucesión de números enteros no negativos que se conoce con el nombre de Sucesión de Fibonacci, en honor al matemático italiano Leonardo de Pisa (1170 – 1240), apodado como Fibonacci. Inicia con los números 0 y 1, y cada término se obtiene sumando los dos anteriores. De esta manera se logra entonces la sucesión:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… .

Con esta sucesión Fibonacci describió cómo crece una población de conejos a partir de una pareja (procreando al mes de existencia) y dando a luz a una nueva pareja tras un mes de gestación, alcanzando los 144 en un año.

La sucesión de Fibonacci se usa también para describir múltiples fenómenos y el cociente entre dos números consecutivos de esta sucesión tiende al número áureo Phi. Una propiedad útil de la sucesión de Fibonacci es la que permite pasar de millas a kilómetros en forma aproximada, ya que una milla es aproximadamente igual a φ kilómetros. Entonces:

3 mi ≃ 5 km

5 mi ≃ 8 km

8 mi ≃ 13 km

13 mi ≃ 21 km.

Como puede concluirse: solo los números pueden describir la incomparable perfección que esconde la belleza de la naturaleza. Como lo expresó muy bien el gran Galileo Galilei (1564 – 1642): “Las matemáticas son el alfabeto con el cual Dios ha escrito el universo”.

@MantillaIgnacio