La suma loca de Ramanujan

Srinivasa Ramanujan es sin lugar a dudas el matemático indio más famoso de la historia de las matemáticas. Su corta vida ha sido contada en novelas muy populares como “El contable hindú”, de David Leavitt (Anagrama, 2011) o “El hombre que conocía el infinito”, de Robert Kanigel (Scribner, 1991), llevada exitosamente al cine en  2015 cuando se estrenó la película basada en esta novela, dirigida por Matt Brown. 

Sobre los más conocidos aportes de Ramanujan a las matemáticas, escribí hace un tiempo este artículo https://blogs.elespectador.com/actualidad/ecuaciones-de-opinion/ramanujan-gran-genio-matematico; pero son muchas las cosas que vale la pena mencionar sobre Ramanujan. 

De su abundante legado matemático esta vez he elegido un genial aporte, menos conocido, para compartirles. Se trata de su contribución a las llamadas “q-series”.

En las redes sociales circula la siguiente viñeta y me han preguntado cuál es el chiste que se esconde allí. Eso es justamente lo que trataré de explicar a continuación.

Para los lectores no expertos, empiezo por referirme a las nociones básicas de sumas infinitas o series numéricas. Un buen ejemplo, que resulta interesante de comprender, es el que se conoce como la paradoja de Zenón, planteada por Zenón de Elea hace ya 2500 años al afirmar que siendo Aquiles tan rápido, corriendo detrás de una tortuga, nunca la alcanzaría porque cuando él recorre la distancia S que lo separa inicialmente de la tortuga, ésta habrá recorrido otra distancia, que aunque es menor, es una nueva distancia que debe recorrer Aquiles y cuando lo haya logrado, la tortuga nuevamente se ha alejado y así sucesivamente. 

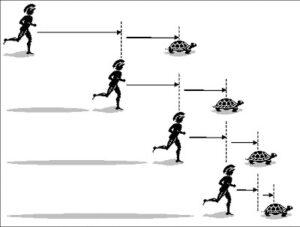
Si suponemos que cuando Aquiles recorre la distancia S, la tortuga avanza la mitad, es decir una distancia igual a S/2, entonces Aquiles estará a una distancia S/2 de la tortuga después de recorrer la distancia S; y cuando avance la distancia S/2, ya la tortuga estará a una distancia igual a S/4, y así sucesivamente, de tal manera que la distancia entre Aquiles y la tortuga siempre será mayor que cero. 

Pero todos sabemos que si Aquiles corre a una velocidad constante, alcanzará a la tortuga y que por lo tanto su recorrido total debe ser finito; es decir que Aquiles va a recorrer la suma de estas distancias en un tiempo finito, es decir que

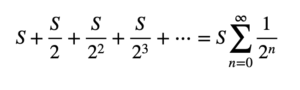
debe ser finito. Hoy sabemos que 

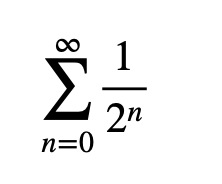
es una serie geométrica convergente a 2, luego Aquiles alcanzará la tortuga recorriendo una distancia finita, en un tiempo finito porque la suma total, aunque tiene infinitos sumandos y  es reconocida como una suma infinita, tiene un resultado finito y no hay paradoja.

Pero cuando una suma no converge, es decir cuando la suma de todos los términos es infinita o no tiene un limite fijo, la situación es diferente, como por ejemplo:

1 – 1 + 1 – 1 + 1 – + ··· .

Una forma de sumar podría ser:

(1 – 1) + (1 – 1) + (1 – 1) + ··· = 0 + 0 + 0 + ··· = 0.

Pero otra forma de sumar puede ser:

1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + ··· = 1 + 0 + 0 + 0 + ··· = 1.

¿Cuál es la correcta? Obviamente podríamos también agrupar sumandos, reordenar y obtener como resultado un número entero cualquiera, lo que indica que no hay un único valor ni uno que sea mejor resultado que otros. Como se observa, tratar con series no es nada trivial y si estas divergen, su tratamiento es muy difícil.

Lo anterior para poner en contexto la fórmula que escribió Ramanujan en su famosa carta, dirigida al matemático británico G. H. Hardy el 16 de enero de 1913, en la que aparece una serie divergente, como lo indica la imagen siguiente de un fragmento conservado de esa carta (fuente: La Gaceta de la Real Sociedad Matemática Española, Vol. 23 (2020), Núm. 2):

El fragmento de la carta de Ramanujan dice que:

“Tengo teoremas sobre series divergentes, teoremas para calcular los valores convergentes correspondientes a las series divergentes […]”

¿Cómo puede esa tercera suma de la imagen, de números todos positivos, dar como resultado un número negativo?  En el lugar de Hardy, cualquier matemático hubiese creído que se trataba de un loco que estaba escribiendo basura. Pero por fortuna esa carta llegó a las manos de Hardy quien era seguramente el matemático inglés más importante de esa época. Él entendió de qué se trataba el asunto y tuvo el acierto de considerar a Ramanujan como un genio para que pudiese obtener una beca para estudiar y trabajar en Cambridge con él.

Pero volvamos sobre la suma de marras en la que a medida que sumamos términos obtendremos un número cada vez más grande. Puesto que 

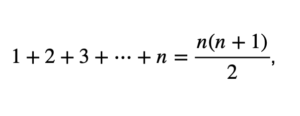
entonces, cuando n tiende a infinito, la suma  

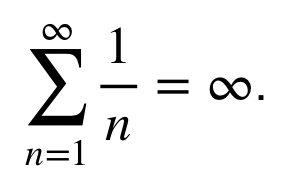
¿Cómo obtuvo entonces Ramanujan ese resultado tan extraño e inverosímil a primera vista?

Para entender el resultado de Ramanujan hay que conocer una serie que se estudia en el Cálculo Diferencial e Integral, conocida como la fórmula de Euler-Maclaurin. Se trata de una serie que involucra una función f(x) que cumple condiciones especiales; una serie que tiene unos coeficientes conocidos como números de Bernoulli

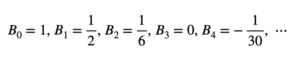
y una constante C que se llama frecuentemente la constante de la serie; esta es una constante que sólo depende de la función f y se puede usar para definir la suma cuando la serie es divergente. Justo esa es la definición que usó Ramanujan. En efecto, si la función es f(x) = x, esa constante C define la suma y resulta ser 

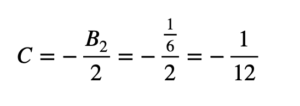
Hay una manera más sencilla de llegar a lo mismo. A continuación lo desarrollo para quienes deseen conocerlo:

Sea

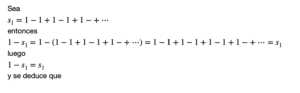
y así obtenemos el valor dado por Ramanujan:

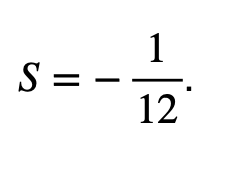
De todo lo anterior se puede observar que tratar una suma de infinitos números no es un problema sencillo; como lo dijo el gran matemático noruego Niels H. Abel en 1826: «Las series divergentes son la invención del diablo, y es vergonzoso basar en ellas cualquier demostración».

Así que no podemos escandalizarnos por el valor que Ramanujan dio a esta serie y tal como lo hizo Hardy, es mejor tomar en serio la respuesta al igual que debemos hacer los profesores al tomarnos el trabajo de descubrir la razón por la que un estudiante obtiene una respuesta aparentemente descabellada porque es posible que estemos frente a un genio.

@MantillaIgnacio