Primicia en el mundo de las matemáticas

Desde octubre del año pasado he recibido decenas de mensajes que contienen vínculos a artículos relacionados con una noticia que los amigos remitentes saben que es de mi interés. He leído con gran entusiasmo todos los artículos recibidos, pues para cualquier matemático los titulares que anuncian nuevos descubrimientos son, sin duda, fuente de curiosidad que provoca su inmediata lectura. Algunos de los artículos mencionados aparecen bajo titulares como los siguientes:

• “Dos matemáticos descubren una nueva forma de contar números primos”
  
• “Dos matemáticos han resuelto un rompecabezas de números primos que parecía imposible descifrar”
  
• “Dos matemáticos encuentran un nuevo método para identificar los números primos”
  
• “Dos matemáticos logran resolver un problema con 2.300 años de antigüedad
  
• “Inventan una fórmula para resolver un dilema matemático que tenía siglos sin resolverse”
  
• “Matemáticos descubren una nueva forma de contar números primos”
  

Y a finales del mes de abril la Universidad de Columbia publica, entre las noticias relevantes de la institución, un artículo titulado:

“Un profesor de matemáticas tiene un nuevo hallazgo sobre los números primos”.

Este último es, a mi juicio, el titular más apropiado o mejor ajustado a la buena noticia que voy a compartirles, pero antes quiero poner en contexto el tema.

Como se sabe, alrededor del año 300 a. C., Euclides demostró que hay una cantidad infinita de números primos (números naturales, mayores que 1, que solo son divisibles por 1 y por sí mismos), además con el aporte de una bella prueba, de las mejores y más ilustrativas usando el método de reducción al absurdo, consistente en suponer que hay una cantidad finita de números primos y llegando a una contradicción.  

Pero no hay una fórmula que nos dé todos los primos, tampoco existe una fórmula que, como si se tratase de una máquina especial, pueda recibir unos números de entrada, elegidos al azar, y mediante algún proceso logre transformarlos para producir únicamente primos de cierta clase. 

Desde Eratóstenes, hace unos 2.200 años, se conoce una criba que lleva su nombre y con la cual es posible conocer todos los primos menores que un natural dado (es un buen ejercicio de programación hoy en día); ese es ya un gran logro.

Uno de los grandes retos matemáticos ha sido encontrar funciones polinómicas que arrojen solo números primos. Grandes matemáticos como Euler lo han intentado, su propuesta fue el polinomio:

P(n) = n² + n + 41 

el cual arroja un número primo para todo n entre 0 y 39. Siendo 41 el primo más pequeño que nos genera y 1601 el más grande.

En 2006, J. Brox encontró el polinomio

P(n) = 6n² – 342n + 4903

que arroja números primos para n entre 0 y 57.

Hoy se sabe, y ha sido demostrado, que no es posible encontrar un polinomio que arroje solo números primos.

Los números primos que se consiguen usando algunas fórmulas o que en general siguen algún patrón han sido clasificados ampliamante, como puede deducirse del artículo que compartí recientemente (ver https://blogs.elespectador.com/actualidad/ecuaciones-de-opinion/los-nombres-de-los-numeros/).

Hay un buen grupo de conjeturas en torno a los números primos que se constituyen en retos matemáticos sumamente difíciles; tal vez la más famosa es la que se conoce como Conjetura de Goldbach, que aparece formulada en 1740 por el matemático alemán Christian Goldbach, quien envió una carta al matemático más destacado de la época, Leonhard Euler, preguntándole si todo número par mayor que 2 es la suma de dos primos. Actualmente, más de 250 años después, aunque se sospecha que la respuesta es afirmativa, no hay una demostración. 

Volviendo a la noticia, de acuerdo con el anuncio de algunos de los titulares presentados arriba, se podría llegar a pensar que se ha descubierto una fórmula insospechada para encontrar primos, pero esto induce a un error y no es propiamente lo que corresponde al importante hallazgo que comparto a continuación.

En octubre del año pasado dos matemáticos –el británico Ben Green, profesor de la Universidad de Oxford, y Mehtaab Sawhney, de origen indio, recientemente vinculado como profesor de la Universidad de Columbia, considerado hoy uno de los matemáticos menores de 30 años más brillantes del mundo– publicaron un artículo en el que logran demostrar que existen infinitos números primos de la forma 

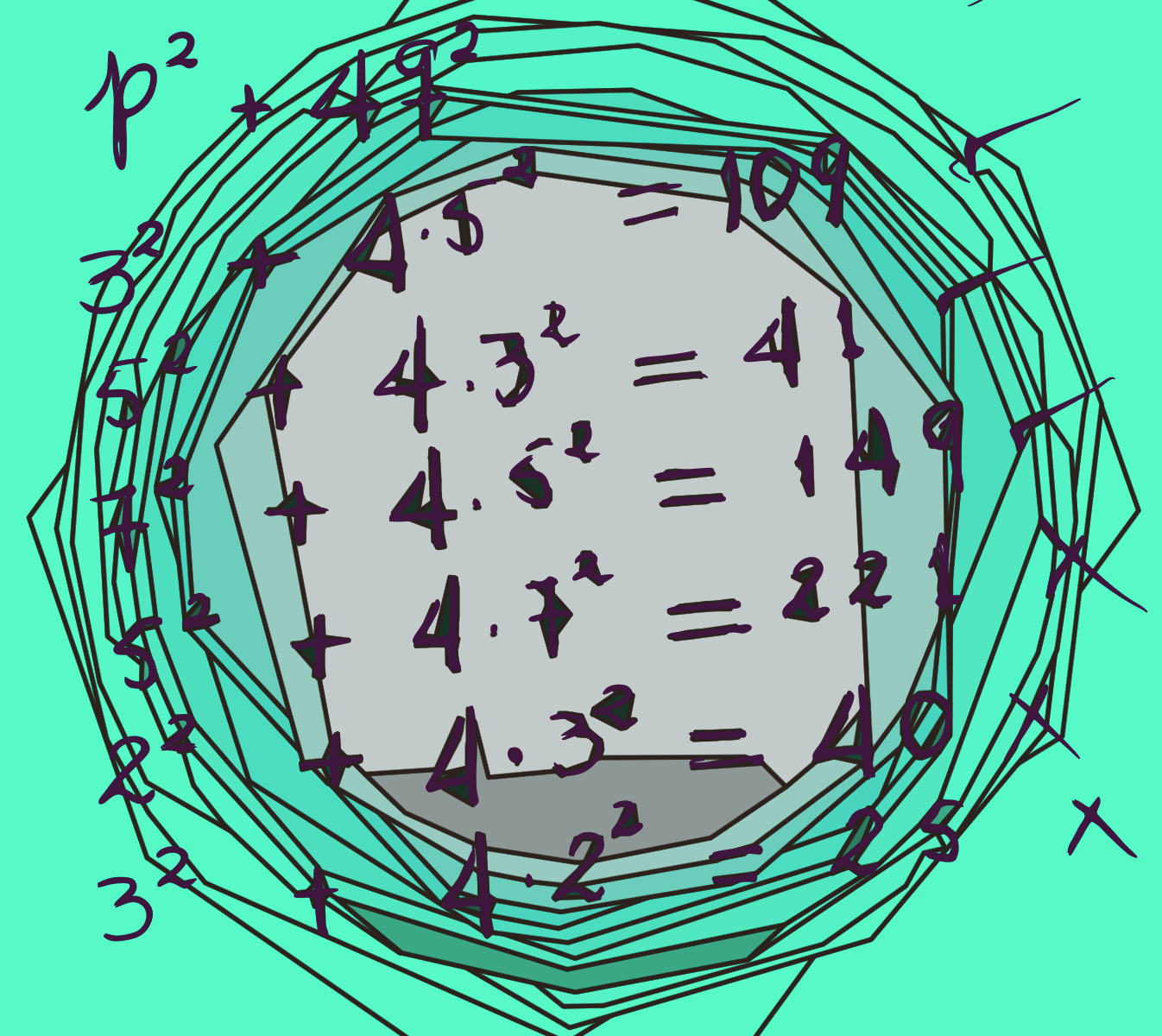
p² + 4q² donde tanto p como q también son primos.

A manera de ejemplo, 

5² + 4·2² = 41,  3² + 4·5² =109

son primos que siguen ese patrón. Pero no hay que confundir este resultado con una falsa generalización; no es cierto que con todo par de primos p y q se consiga un nuevo primo de esta forma, basta observar que 

3² + 4·2² = 25 

no es primo.

El resultado es, sin embargo, sumamente relevante y lleva a una nueva clase de números primos, un subconjunto que es infinito y esa demostración tiene, por lo tanto, un valor especial, porque las afirmaciones sobre la cantidad de números primos que siguen un patrón particular son sumamente valiosas y especialmente difíciles de demostrar. Por ejemplo, en el siglo XIX, Peter G. L. Dirichlet demostró un teorema sobre progresiones aritméticas del que se deduce un corolario muy valioso con el que se demuestra que existen infinitos primos que terminan en 7.

La primicia matemática que se ha difundido es también un buen ejemplo que muestra la dificultad que tienen los medios informativos para presentar titulares que respeten la precisión antes que la atracción.

Estaré atento a nuevas buenas noticias sobre esta fascinante área de la Teoría de Números para poder compartirle a los lectores material de lectura que les aleje por unos minutos de la cotidianidad.

@MantillaIgnacio