La increíble historia detrás de un famoso problema de probabilidad

Hay circunstancias por las que algunos problemas de matemáticas se vuelven famosos, como ocurre con las personas que se convierten en celebridades por algún don o por un hecho que de un día para otro les cambia la vida. Este es el caso del famoso problema de probabilidad, conocido bajo el nombre de “paradoja”, “problema” o “dilema” de Monty Hall. Un bello ejercicio que ya se incluye en los cursos regulares de probabilidad.

Aunque el problema fue planteado en 1959 en una primera versión, publicada en la revista de divulgación científica Scientific American, por el gran divulgador matemático Martin Gardner (1914 -2010), fue gracias a un programa de concurso en la televisión estadounidense, llamado Let’s make a deal (que estuvo al aire entre 1963 y 1990), que el problema se divulgó con el nombre del presentador de ese programa: Monty Hall.

El problema de Monty Hall es el siguiente: suponga que está usted participando en un concurso y le han dado a elegir entre tres puertas. Detrás de una de ellas hay un carro nuevo y detrás de cada una de las otras hay una cabra, pero usted no sabe qué hay detrás de cada puerta; su premio será lo que haya detrás de la puerta que elija. Si usted ha elegido una puerta y antes de abrirla, el presentador, que sabe lo que hay detrás de cada puerta, abre una y deja ver detrás de ella a una cabra y luego pregunta: «¿se queda usted con la puerta elegida o quiere cambiar su elección?», ¿es mejor cambiar de puerta?

La intuición de la mayoría es que una vez descartada una puerta, la que el presentador ha destapado con la cabra detrás, la probabilidad de ganarse el carro es 1/2, pues al estar el premio detrás de alguna de las otras dos puertas, se tiene una opción favorable de dos posibles y por lo tanto da igual cambiar la elección inicial que no hacerlo. 

Sin embargo, la respuesta al problema se convirtió en una verdadera “bomba matemática” en 1990, cuando Marilyn vos Savant dio una respuesta distinta en la revista Parade, en su columna semanal llamada Ask Marilyn donde resuelve problemas de diversas temáticas. En efecto: Marilyn (nacida en 1946), famosa mujer a nivel mundial por ostentar el honor de ser la persona con el Cociente Intelectual (CI) más alto del planeta, con 228, había respondido una carta de Craig F. Whitaker, quien le pedía su consejo ante el dilema de cambiar o no la elección inicial de una puerta. La respuesta de Marilyn fue la correcta, pero sorprendente: es mejor cambiar de puerta para tener una mayor probabilidad de ganarse el carro.

Nadie imaginó lo que ocurriría después de la publicación de su columna con esa respuesta. En la redacción de Parade se recibieron miles de cartas señalando que la respuesta de Marilyn era incorrecta. En una de estas cartas le decían: “Tú eres la cabra”. En ellas se daba como respuesta correcta que tanto quedándose con la puerta elegida al principio como cambiando de puerta, la probabilidad era de 1/2. 

Entre los remitentes y críticos había algunos matemáticos asombrados y decepcionados del error debido a la poca formación matemática de la columnista. Se menciona que uno de ellos fue el matemático húngaro Paul Erdös (1913 – 1996), uno de los más importantes matemáticos del siglo XX, quien al ser interrogado sobre la respuesta de Marilyn expresó: “esto es imposible”. Posteriormente Erdös, como los demás, admitió que era él quien estaba equivocado.

Pero veamos por qué la respuesta correcta es: cambiando la elección inicial, aumenta la probabilidad de ganar. 

Imaginemos que el carro está detrás de la puerta #3 y consideremos las tres posibilidades que tiene el concursante: escoger la puerta #1, la #2 o la #3 y supongamos que el concursante siempre cambia la puerta elegida inicialmente, después de que le enseñen la que tiene la cabra detrás. Vamos a calcular la probabilidad de ganar el carro.

PRIMERA POSIBILIDAD. Escoge la puerta #1. 

En ese caso, el presentador no puede enseñar la puerta #3, ya que detrás está el carro; y tampoco puede mostrar la puerta #1, pues ha sido la escogida por el concursante. Por lo tanto, debe enseñar la puerta #2. La decisión del concursante, de cambiar la puerta elegida originalmente, obliga entonces a elegir ahora la puerta #3, pues ya vio la cabra detrás de la #2 y había elegido inicialmente la #1. En este caso el concursante gana, pues es detrás de la puerta #3 que se encuentra el carro.

En resumen, si elige la puerta #1 y cambia, entonces gana.

SEGUNDA POSIBILIDAD. Escoge la puerta #2.

En este caso, el presentador solo puede mostrar la puerta #1 con la cabra detrás. Por lo tanto al cambiar hay que elegir la puerta #3 y el concursante nuevamente gana.

En resumen, si elige la puerta #2 y cambia, entonces gana.

TERCERA POSIBILIDAD. Escoge la puerta #3.

El presentador bebe mostrar la puerta #1 o la #2, ambas con una cabra atrás. Así que al cambiar el concursante pierde.

En resumen, si elige la puerta #3 y cambia, entonces pierde.

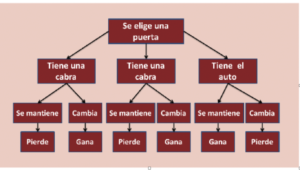
Ahora bien; como se puede concluir, examinando las tres posibilidades anteriores, al cambiar la puerta inicialmente elegida, el concursante puede ganar en dos de las tres posibilidades, es decir que la probabilidad de ganar es de 2/3, mientras que con la decisión de no hacerlo, la probabilidad de ganar es apenas de 1/3, como se puede observar en el siguiente esquema que ilustra cómo, manteniendo la elección inicial, solo gana en una de las tres posibilidades.