Euler y el problema de Basilea

Como bien es conocido, el suizo Leonard Euler (1707-1783) ha sido el matemático más prolífico de la historia, a tal punto, que a mediados del siglo XIX, más de 50 años después de su muerte, su trabajo aún no se había acabado de publicar. En casi todas las áreas de las matemáticas, desde la Teoría de Números hasta las Ecuaciones Diferenciales, se encuentra la influencia transformadora de sus ideas, por la que muchas llevan su nombre.

Pero la obra de Euler no solo es abundante, también es profunda, propia de un genio que generosamente y sin descanso mostró su talento en cada nuevo proyecto, que resolvió problemas que se creía que eran insolubles, desarrollando una espléndida carrera y gozando de una extraordinaria reputación. 

Aun cuando Euler perdió la visión de uno de sus ojos antes de cumplir 30 años de edad y sus últimos 15 años de vida estuvo completamente ciego, sus discípulos e hijos ayudaron para que no nos privásemos de sus aportes en esos últimos años; ellos escribían exactamente lo que les dictaba Euler y su facilidad para los números y especialmente su capacidad de realizar mentalmente cálculos con grandes números fue aún más notable.

Uno de los problemas que resolvió Euler, y que sirve de ejemplo para reconocer su talento, es el conocido bajo el nombre de “Problema de Basilea”, que consiste en determinar cuál es el valor exacto de la suma de los cuadrados de los inversos de todos los números enteros positivos, es decir, calcular:

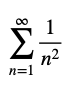
Este problema había sido planteado por primera vez en 1644, en la obra “Novae Quadraturae Arithmeticae” de Pietro Mengoli, y antes de Euler fue muy popular porque grandes matemáticos como Jakob Bernoulli, Johann Bernoulli, Daniel Bernoulli, Gottfried Leibniz, James Stirling, Abraham de Moivre, John Wallis, entre otros, intentaron sin éxito dar con su solución; lo que había convertido el problema en un famoso reto matemático. 

En 1735, con 28 años de edad, Leonard Euler encontró la solución del problema y el 5 de diciembre del mismo año, la presentó en la Academia de San Petersburgo. El problema acabó teniendo nombre propio: “Problema de Basilea” porque era esta ciudad suiza de residencia tanto de los Bernoulli como de Euler.

La solución dada por Euler se basa en una idea sumamente ingeniosa. Considera la función seno que toma infinitas veces el mismo valor, como si fuese un polinomio, imaginando entonces un supuesto “polinomio infinito” con infinitas raíces. Euler conocía el desarrollo de la función seno en serie de Taylor, que es de donde parte: 

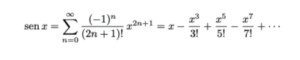
Puesto que la función seno se anula en los múltiplos de π, se expresa esta suma como: 

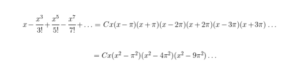
Como para cada n se tiene que

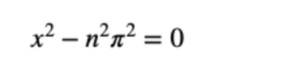
puede entonces escribirse esta expresión, como si se tratase de un polinomio, en la forma

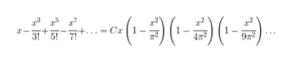
Euler dividió luego esta expresión por x obteniendo: 

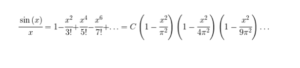que como se sabe, no se anula en cero (en efecto, el límite cuando x tiende a cero vale 1, o sea que C = 1), pero que para todos los demás valores, tiene exactamente las mismas raíces de la función seno, o sea los múltiplos de π. 

Euler pudo entonces expresar la suma como producto infinito, al igual que se hace con los polinomios, pero en este punto Euler recibió bastantes críticas a su metodología expuesta, resaltándole la falta de rigor, ya que el tratamiento de un producto infinito como si fuese un polinomio no era aceptable. Johann Bernoulli presentó como contraejemplo la función 

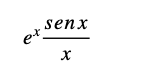
que tiene las mismas raíces y sin embargo la expresión como producto infinito es diferente. No obstante, la intuición que dominaba a Euler, no le hizo desistir de su metodología, y aunque hubiese cosas pendientes por demostrar, sabía que el resultado que iba obteniendo con valores aproximados le conducían a la solución correcta.

Euler disponía de estas dos expresiones diferentes para la misma función,

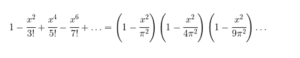
entonces igualó los coeficientes de los términos del mismo grado como si se tratase de comparar dos polinomios, pero quedándose solamente con el coeficiente de x², pues los demás no los necesitaba. Al deshacer los paréntesis en la expresión e igualar, la comparación del coeficiente de x² en la izquierda de la igualdad con los coeficientes resultantes de x², a la derecha, lleva a la siguiente igualdad:

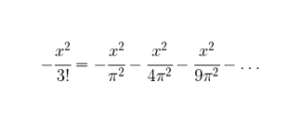
La euforia que podemos imaginar que sintió Euler al ver que el problema estaba prácticamente resuelto debió ser monumental, pues con esto:

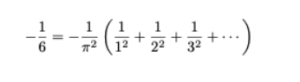
y por lo tanto la solución al problema de Basilea es:   

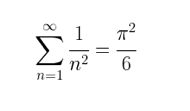
¡EUREKA!

En esta solución, como lo hemos dicho, Euler utiliza resultados no demostrados, que posteriormente justificaría formalmente. Después de Euler vendrían otras demostraciones, pero ya con la certeza de conocer el valor encontrado por Euler al cual converge esa serie y que sorprendentemente incluye al número π.

Este bello problema y el procedimiento usado por Euler muestra no solo su genialidad para encontrar caminos inimaginables para resolver problemas, sino la importancia de tener fe en la intuición que nos guía muchas veces hasta la terquedad, cuando abordamos problemas o realizamos cálculos, esa intuición que no debe permitirnos desviar nuestra atención ante posibles generalizaciones aparentemente indebidas que pueden justificarse después.

@MantillaIgnacio