En defensa de los logaritmos

Las nuevas generaciones seguramente no conocieron las “tablas de logaritmos”, unos libritos pequeños llenos de números con muchas cifras decimales, organizados en filas y columnas. Esas tablas formaban parte del equipo de trabajo permanente que debíamos tener siempre a mano los estudiantes de ciencias o ingeniería, era una herramienta indispensable para los cálculos aritméticos a la hora de presentar exámenes, pues sin ella era imposible dar con las respuestas a los problemas que había que resolver en poco tiempo para obtener una buena calificación.

Tal vez hoy parezcan una herramienta tortuosa y difícil de dominar, pero si comparamos las tablas de logaritmos con los instrumentos de apoyo a los que se podía acudir antes de su aparición, podemos afirmar que fuimos afortunados de disponer de este maravilloso invento. Siempre me he preguntado cómo sería de tediosa la tarea de realizar operaciones aritméticas en la Edad Media por ejemplo. La siguiente frase del eminente matemático francés Pierre-Simon Laplace (1749-1827) así lo demuestra: “Con la reducción del trabajo de varios meses de cálculo a unos pocos días, el invento de los logaritmos parece haber duplicado la vida de los astrónomos”.

De tal magnitud fue el descubrimiento de los logaritmos. Este tuvo lugar solo hasta el siglo XVII y significó un gran avance para las matemáticas en particular y para las ciencias en general, como veremos. Es una herramienta que hoy en día está disponible en cualquier calculadora de bolsillo o teléfono celular común y que tal vez, por eso mismo, no apreciamos en todo su inmenso valor.

El gran matemático escocés John Napier de Merchiston (1550-1617), llamado también Johannes Neper es conocido como el padre de los logaritmos; fue el primero en definirlos y se encargó de popularizarlos; también introdujo el uso de la coma decimal para los cálculos numéricos. Neper fue un matemático que se preocupó especialmente por simplificar los cálculos, por eso ideó también un ábaco, conocido como el “Ábaco Neperiano”. Se trata de un ingenioso invento para realizar operaciones aritméticas, pues permite convertir productos en sumas y divisiones en restas. Para los lectores interesados en el funcionamiento de este sorprendente artefacto, pueden leer el blog https://divermates.es/2014/10/13/abaco-neperiano/. Y los más curiosos, si alguna vez tienen la oportunidad de visitar la ciudad de Bonn en Alemania, pueden deleitarse con un ejemplar y otros instrumentos derivados de este ábaco en el fantástico museo “El Arithmeum”, de esa ciudad. Un modelo expuesto del “Ábaco Neperiano” puede admirarse también en el Museo Arqueológico de Madrid en España.

Pero retomemos el aporte de Neper con la invención de los logaritmos y recordemos qué es un logaritmo. En general, el logaritmo en base b de un número positivo N es la potencia p a la que hay que elevar la base b para que sea igual al número N. 

Lo primero que hay que fijar es la base del logaritmo, que siempre es positiva porque es imposible conseguir un número positivo N multiplicando p veces un número negativo. 

Si la base es 2 por ejemplo, y denotamos con “log₂” al logaritmo en base 2, entonces, a manera de ejemplo:

log₂(32) = 5 

porque 5 es la potencia a la que debe elevarse la base 2 para obtener el número 32; o simplemente porque 

2⁵ = 32. 

Cuando la base es 10 los llamamos logaritmos decimales y se acostumbra escribir simplemente log. Así por ejemplo:

log(1000) = 3.

Un dato curioso es el del matemático y reverendo inglés Henry Briggs, quien publicó en 1624 la primera tabla con los logaritmos decimales de treinta mil números naturales, y cada uno contenía catorce cifras decimales; un trabajo descomunal para la época. Es esta la razón por la que también se les llama “logaritmos de Briggs” a los logaritmos decimales.

Y una base muy importante, bastante utilizada para los logaritmos, es el número de Euler e, que como sabemos es un número irracional y por lo tanto tiene infinitas cifras decimales:

e ≈ 2,71828… 

Cuando la base del logaritmo es este número, el logaritmo se denomina “logaritmo neperiano” en honor a Neper, o también “logaritmo natural” y se denota simplemente como ln, por esa razón

ln(e) = 1.

La utilidad de los logaritmos es muy amplia ya que permiten manejar escalas con cifras muy distantes (quizá algunos lectores recuerden las tareas del colegio que había que presentar en “papel logarítmico”), así por ejemplo para representar en una misma gráfica valores que inician en una escala marcada con el número 10 en un eje y alcanzan el valor de 100.000 en el mismo eje, sería imposible visualizarlos sin pasar a una escala logarítmica que transforma el intervalo entre 10 y 100.000 en otro que va de 1 a 5, cuando se toman los correspondientes logaritmos. 

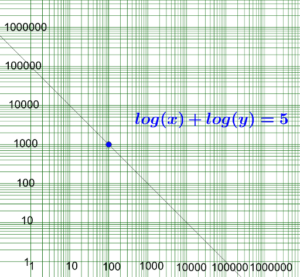
(Imagen tomada de GeoGebra)

Para comprenderlo mejor recordemos que en la escala de Richter, usada para estimar la intensidad de los temblores de tierra, cada “grado” adicional indica que se multiplica por 10 el valor anterior. Esto significa que un temblor de grado 6 es 100 veces más intenso que el temblor de grado 4 y el terremoto de grado 8 será 10.000 veces más intenso que el temblor de 4. Así, la escala de Richter nos presenta en este caso pocas divisiones, de 4 a 8, para ir de 100 a 10.000.

En realidad en una escala lineal se suma en cada paso, mientras que en una escala logarítmica cada paso corresponde a una multiplicación; esa es una de las propiedades más importantes de los logaritmos, “transformar” productos en sumas (como en el ábaco de Neper):

log(x·y) = log(x) + log(y),

es una especie de telescopio matemático inventado hace 400 años para que podamos apreciar y dominar los cálculos aritméticos como si estuviéramos haciendo “zoom”. De igual manera, en ese sentido los logaritmos transforman divisiones en restas:

log(x/y) = log(x) – log(y).

Ahora bien, si recordamos el significado de un “crecimiento exponencial” que es el que se presenta en los fenómenos naturales que describen el crecimiento de poblaciones biológicas, o el que aparece en el cálculo de intereses bancarios, entre otros muchos ejemplos, podemos imaginar inmediatamente la utilidad que tiene el uso de los logaritmos naturales (de base e) para describir esos crecimientos que involucran a la función exponencial. 

Será tema de otros artículos desarrollar algunos ejemplos para ilustrar en detalle la sorprendente utilidad de los logaritmos.

@MantillaIgnacio