¿De dónde viene el número e?

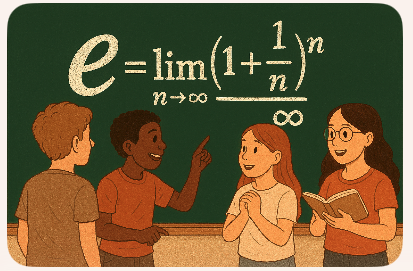
Es tan importante el número e o Número de Euler como lo es el número π, pero a π nos lo presentan desde el colegio, comúnmente en el primer curso que aborda conceptos de Geometría Plana y es fácil aceptarlo como la constante que resulta de dividir la longitud de una circunferencia entre su diámetro; en cambio, especialmente por la dificultad de definir el número e a veces se opta por evitarlo y es así como hay quienes terminan el bachillerato sin ni siquiera haberlo oído mencionar. Y quienes lo conocen, en su mayoría saben que se trata de un número irracional entre 2 y 3; algunos más, saben incluso, de memoria, las primeras cifras decimales:

e ≈ 2,7182818285,

y la mayoría de quienes lo usan han aprendido que también es la base de los “logaritmos naturales o neperianos”.

La importancia del Número de Euler e, es la que quiero destacar hoy, dedicando esta nota para contarles, o recordarles, quién es e, de dónde salió y mostrándoles por qué merece un artículo dedicado solamente a él. 

Las primeras referencias de la constante que posteriormente se llamaría e fueron publicadas a comienzos del siglo XVII con el trabajo sobre logaritmos de John Napier (1550-1617) quien observó que los cálculos que involucraban números muy grandes y muy pequeños eran una tarea demasiado difícil, así que comenzó desarrollando un sistema de logaritmos para simplificar los cálculos aritméticos al permitir que la ardua tarea de la multiplicación se redujera a sumas. En otras palabras, Napier descubrió un atajo para calcular exponentes.

Su aplicación inicial tuvo trascendencia en Astronomía principalmente, campo en el que el uso de los logaritmos facilitó los tediosos cálculos a tal punto que dos siglos después, el gran matemático francés Pierre-Simon Laplace (1749-1827) expresó: “Con la reducción del trabajo de varios meses de cálculo a unos pocos días, el invento de los logaritmos parece haber duplicado la vida de los astrónomos”. 

Sin embargo no fue a través de los logaritmos que se descubrió e, y no fue sino hasta 1683, del estudio del interés compuesto que llevó a cabo Jacob Bernoulli, que apareció el número e. A propósito del interés compuesto, se le atribuye a Albert Einstein la cita según la cual: “el interés compuesto es la octava maravilla del mundo… Aquel que lo entiende, gana dinero; aquel que no, lo paga”. Seguramente es otra más de las muchas citas que se le atribuyen a Einstein, sin ser de su autoría.

En detalle, la aparición de e puede explicarse en forma sencilla si se piensa que el interés que se gana por un préstamo, que se recibe al final del tiempo pactado, puede distribuirse para ir cobrándolo cada cierto tiempo de manera que sobre esos rendimientos se cobren también los intereses. 

Más precisamente, con un ejemplo, podemos llegar al número e de la siguiente manera: supongamos que se invierte una unidad monetaria (UM) con un interés del 100% cada 8 años, es decir que el capital inicial se duplica al cabo de un octenio. Pero si en lugar de esto se divide el interés en dos partes y se pagan esos intereses dos veces en el octenio, cada cuatrienio, la cantidad obtenida en el primer cuatrienio es:

 (1 + 1/2) = 1,5 UM 

y en el octenio ahora el total es de: 

(1 +1/2) · (1 + 1/2)  = 2,25 UM

obteniéndose entonces una suma que supera las 2 UM que se reciben con un solo pago de intereses.

Y si ahora dividimos el octenio en 4 períodos (bienios), al igual que la tasa de interés, se obtienen

 (1 + 1/4) · (1 + 1/4) · (1 + 1/4) · (1 + 1/4) =  2,4414… UM

que aumenta aún más la suma final obtenida con uno o dos pagos de intereses.

Y si lo pacto anual, tenemos que el valor al final del octenio es:

(1 + 1/8)⁸ ≈ 2,57 UM

Se observa cómo, a medida que se aumenta la cantidad de períodos de pago, reduciendo proporcionalmente la tasa de interés en el período, aumenta también el total de unidades monetarias que se reciben al final del octenio. Entonces surge la pregunta, ¿crecerá indefinidamente, al infinito? Para obtener esa respuesta hay que imaginar n períodos de capitalización y calcular: 

que es el tope al que podrían crecer las UM. Y ese límite es justamente igual a

2,7182818285… = e.

Bernoulli utilizó el teorema del binomio para aproximar esta constante y esa fue la primera aproximación de e de la historia; sin embargo Bernoulli no relacionó ese número con los logaritmos y no investigó más esta constante, pero lo cierto es que ese trabajo de Bernoulli es el que permite afirmar que una inversión de un capital C a una tasa de interés anual R, con interés compuesto, proporcionará entonces Ce^R unidades monetarias al cabo del primer año y Ce^RN al cabo de N años. 

Y podemos volver a preguntarnos cuál es ahora el tiempo necesario para duplicar la inversión. La respuesta se logra igualando

es el tiempo requerido para duplicar la inversión. Si por ejemplo fuese R = 10% anual, entonces eso ocurre en 

N = 6,93147

por lo tanto en 7 años se habrá duplicado la inversión con un interés compuesto del 10% anual.

Pero volviendo al origen de e, la razón por la que se llama número de Euler a e se debe a que Leonard Euler usó esa notación para representar esa constante irracional. Sin embargo, no puede asegurarse que sea por tratarse de la primera letra de su nombre o por ser la primera letra de la palabra francesa “exponentiel”.

Sin embargo, cualquiera haya sido la razón, Euler sí utilizaba la letra e para representar la base del sistema de logaritmos naturales, que aun cuando existían desde un siglo antes, no había sido introducida una notación aceptable. El registro más importante del nombre e aparece en una carta que Euler dirige al matemático alemán Chistian Goldbach en 1731 en la que usa la letra e para referirse a “el número cuyo logaritmo hiperbólico es igual a 1”. Este símbolo fue admitido universalmente desde entonces.

Pero lo más relevante y el indudable merecimiento para que se llame constante o Número de Euler a e radica en los numerosos descubrimientos que hizo Euler sobre las propiedades de e en los años siguientes. En particular demostró que e es un número irracional y que puede escribirse como:

y en 1748, apoyado en el trabajo de Bernoulli sobre interés compuesto, dio a conocer una aproximación extraordinaria para la época, con 18 decimales

e = 2,718281828459045235.

Euler dedujo su conocida identidad, de la que se afirma que es la más bella ecuación matemática:

Como se observa, hay muchas razones para que esta constante lleve asociado el nombre de Euler, como si se tratase de su primera cifra decimal.

En 1873 Charles Hermite demostró que e es un número trascendente, es decir que no es raíz de ningún polinomio con coeficientes enteros no todos nulos. Este es un resultado importante en la historia de las matemáticas, si se tiene en cuenta que la demostración de la trascendencia del número π tardó más tiempo en lograrse, hasta 1882, cuando lo demostró el matemático alemán Ferdinand von Lindemann.

Espero haber contribuido al reconocimiento del número de Euler e, como uno de los grandes números que vale la pena aprender.

@MantillaIgnacio