¡Aténgase al pinochazo y verá!

Los problemas de conteo arrojan, en la mayoría de los casos, unas respuestas sorprendentes y al mismo tiempo nos indican cómo el azar o las cifras anecdóticas no siempre son una buena guía para la toma de decisiones. Así como se tiende a generalizar o a generar pánico a partir de una experiencia o del rumor de una debacle sustentada en un solo caso, así mismo se propaga rápidamente una falsedad y cuesta luego ganar la misma credibilidad con la corrección. Es lo que vivimos a diario con la publicación de noticias falsas.

Las matemáticas pueden ayudar a corregir ciertos anuncios errados, y es precisamente el cálculo de probabilidades una herramienta esencial para tal fin. Hoy quiero compartir justamente un bonito problema cuya solución despeja las dudas sobre las posibilidades de acertar usando solamente el azar cuando se está frente al reto de aprobar un examen con preguntas de selección múltiple.

El problema lo he denominado “problema del pinochazo”, por la palabra con la que llamamos en Colombia esa práctica de algunos estudiantes, que confiados en su buena suerte solamente, contestan las preguntas de selección múltiple adivinando la respuesta, sin detenerse a pensar. Se cree que el origen de la palabra “pinochazo” es el resultado de jugar con las respuestas disponibles, saltando sobre ellas aleatoriamente o en un orden caprichoso y contando en cada una un “pin”: pin 1, pin 2, pin 3, hasta pin 8 y eligiendo esta última como respuesta correcta.

Para explicar las matemáticas que están detrás, voy a usar un ejemplo que ilustre cuál es la probabilidad de aprobar un examen con esta práctica. El problema del ejemplo es el siguiente:

Problema del pinochazo: 

Un examen de selección múltiple contiene 10 preguntas, cada una con 5 respuestas A, B, C, D, E. ¿Cuál es la probabilidad de que un estudiante, contestando todas las preguntas al pinochazo, apruebe el examen acertando 6 o más respuestas correctas?

Empecemos por recordar de cuántas formas podemos elegir grupos de preguntas entre las 10 que conforman el examen. Es fácil aceptar que una sola pregunta la podemos seleccionar de 10 maneras diferentes. Y si queremos escoger 2 de las 10, entonces la cuenta es sencilla, pero hay que tener cuidado de no confundir una permutación con una combinación: en el primer caso, para elegir la primera hay 10 posibilidades y para la segunda, una vez seleccionada la primera, quedan ahora 9 posibilidades. En total

10 x 9 = 90 

formas de seleccionar 2 preguntas de las 10, es decir permutaciones posibles de 2 elementos tomados de un conjunto de 10. Pero en nuestra selección no importa el orden en que se eligieron las dos preguntas; así por ejemplo la pareja formada por la pregunta 4 y la pregunta 7, denotada como (4, 7) es la misma pareja (7, 4), constituida por las mismas dos preguntas, pero seleccionadas en el otro orden. Por lo tanto, en la cuenta inicial que dio como resultado 90, hemos contado dos veces cada selección y debemos ahora entonces dividir por 2 el número total de permutaciones. Así obrtenemos

(10 x 9) / 2 = 45 

formas de combinar 2 de las 10 preguntas.

En general se puede probar que para seleccionar k preguntas de las 10, el número de combinaciones posibles es:

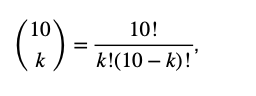
donde el símbolo (!) indica factorial (m! = 1 x 2 x 3 x … x m).

Ahora bien, si cada una de las preguntas tiene como opciones las cinco respuestas A, B, C, D y E, y hay solo una correcta, esto quiere decir que hay una de cinco posibilidades de acertar cada pregunta, es decir que la probabilidad de contestar correctamente una pregunta es de 1/5. Pero esto también indica que la probabilidad de responder erróneamente una pregunta es aún mayor, exactamente de 4/5. 

Con lo expuesto hasta aquí podemos ahora afirmar que la probabilidad de responder exactamente 6 preguntas en forma correcta es:

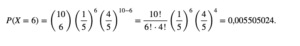
Esto indica que para aprobar con la nota mínima al pinochazo se tiene una probabilidad de apenas el 0,55%.

La probabilidad de responder todas las preguntas en forma incorrecta es de

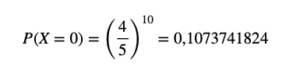
o sea del 10,74%; con lo cual resulta, como bien puede observarse, que es más probable que todas las preguntas se respondan incorrectamente, que acertar y aprobar con el mínimo de 6 buenas.

Para dar respuesta a la pregunta inicial, sobre cuál es la probabilidad de responder 6 o más preguntas correctamente, sumamos las probabilidades así:

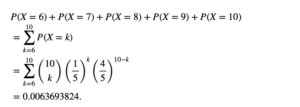
Por lo tanto, la probabilidad de acertar con 6 o más preguntas correctamente, es de apenas 0,64%. 

El pinochazo como estrategia es entonces muy poco aconsejable, la probabilidad de aprobar no alcanza, en ningún caso, al menos el 1%.

Como moraleja: no hay que abandonarse a la suerte para contestar los exámenes de selección múltiple; es mejor estudiar y pensar antes de responder… ¡aténgase al pinochazo y verá!

@MantillaIgnacio