La modelación mental o formalismo: creación extraordinaria de la cultura humana

Los cerebros de los organismos vivos son en esencia máquinas diseñadas por la evolución para representar la realidad exterior. Son el resultado de 4000 millones de años de presión evolutiva, que somete a toda forma de vida a una lucha incesante por la supervivencia, en cada momento, en cada medio, en cada nicho ecológico.

En los albores de la vida, los primeros cerebros no eran más que pequeños conjuntos de neuronas capaces de interpretar la dirección de un foco de luz, y poner así en marcha un flagelo que podía guiar a su poseedor a la fuente del alimento, abundante en la superficie de los océanos primigenios. Esas mismas estructuras, simples en un comienzo, se fueron convirtiendo en máquinas más intricadas, a medida que los primitivos fotorreceptores se convertían en ojos más y más complejos. El mundo binario de la luz y la oscuridad fue cediendo en un universo de formas, fondos, colores, texturas… Cada una de las cuatro dimensiones, tiempo y espacio, debieron ser representadas en redes neuronales de un mayor tamaño, en cableados de axones y dendritas que en su conjunto constituyen una representación interior abstracta, burda y pobremente aproximada de ese fantasma elusivo que llamamos “mundo exterior”.

En palabras del neurocientífico Rodolfo Llinás, “Tenemos ojos que evolucionaron para generar imágenes del mundo externo mediante las propiedades de rebote de los fotones. Pero ¿qué es una imagen? Una imagen es una simplificación de la realidad. El cerebro constantemente simplifica la realidad; más aún, simplifica el mundo externo, pero en forma muy útil. Una imagen es una representación simplificada del mundo externo escrita en forma extraña. Cualquier transducción sensorial es una representación simplificada de un universal emanado del mundo externo. El cerebro es muy Kantiano en cuanto a la esencia de sus operaciones”.

El cerebro, no sabemos aún cómo lo hace, le presenta a ese objeto etéreo e inaprensible que llamamos nuestro “yo” una representación (nuestra “la realidad”) del mundo en que habitamos. Sin embargo, en el cerebro de los humanos, y en menor medida en el de algunos otros mamíferos superiores, ha ocurrido algo inusitado: esa misma representación interna se expresa de forma exterior, mecanismo sin el cual sería imposible la comunicación. El lenguaje mismo, como bien señala el gran lingüista Noam Chomsky, no apareció con gruñidos y gestos guturales, como algunos de manera ingenua suponen, sino que fue probablemente en sus orígenes una extensión de ese “mentalés” interno que debió aparecer primero en el alambrado de la red neuronal para hacer compatible una misma realidad entre miembros de una misma especie.

Pero el lenguaje no se limita a nuestra capacidad lingüística. Los símbolos, como pueden ser palabras, pueden ser también objetos abstractos, caracteres creados para representar categorías, relaciones, orden, funcionalidad… Son esos símbolos los que permiten descubrir e inventar nuevos mundos, inalcanzables para nuestros limitados sentidos, extensiones no menos reales de nuestro mundo perceptivo. A esa herramienta los matemáticos la llaman formalismos y los filósofos, modelación mental. Toda la civilización humana, en gran medida, es producto de esa varita “mágica” en manos de todos.

En su libro, Cómo descubrimos los números, el escritor de Isaac Asimov nos ofrece un ejemplo palpable. ¿Cómo le cuenta un cazador a otro que mató un oso hace veinticinco días si desconoce el concepto de “número entero”? Dicha persona podría usar, como hacen los niños, los dedos de las manos para simular veinticinco sucesos consecutivos. Y el mecanismo pronto se agota sin símbolos apropiados cuando lo ocurrido se hace más y más remoto. El uso de piedritas y otros objetos proporciona un primer recurso. No es casual que la palabra “cálculo”, signifique “piedra”, de donde se deriva el verbo “calcular”.

Algunos animales, como los cuervos, pueden hacer representaciones abstractas de los números enteros (positivos y negativos) más pequeños. En un célebre experimento, un hombre entra a una casita de madera que se encuentra justo al lado de un pequeño comedero para el animal. Desde un árbol, el cuervo lo observa. Solo cuando el hombre vuelve a salir, el pájaro se arrima a la comida que allí le dejan. Luego entran dos hombres, y sale solo uno. El cuervo, que sabe que dos menos uno no es cero, y no se arrima a su comida hasta que el segundo hombre decide salir. El experimento se repite con seis, siete y hasta diez hombres que entran a la vez, y luego salen en grupos de dos, de tres… El cuervo lleva sigiloso la contabilidad: 10 menos 2, menos tres… Solo si la cuenta queda en cero el animal se arriesga a entrar. Grupos más númerosos lo confunden; el animal se equivoca cuando su sistema de representación mental rebasa su limitada, aunque extraordinaria capacidad aritmética.

Los sistemas numéricos posicionales son ejemplos paradigmáticos de los primeros formalismos matemáticos. En el sistema decimal, para citar un ejemplo, usamos los dígitos arábigos para representar los primeros enteros hasta el nueve (incluyendo el cero, representación del vacío, de la nada). Luego, a la izquierda, el nuevo dígito representa el número de potencias de diez. El próximo situado más a la izquierda, representa el número de potencias de cien, y así sucesivamente. Las ventajas con respecto al sistema de numeración romano pueden apreciarse cuando es necesario hacer cualquier cómputo medianamente complejo. Por ejemplo, intentemos dividir MDXXXV entre DLIX, usando el sistema de numeración romano.

Otro sistema posicional fue inventado por los Babilonios: en base 60, utilizaba barras para las unidades y cuñas para las potencias de 60. Es increíble, todavía se usa para dividir el círculo en 360 grados.

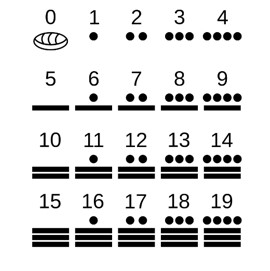
Otro sistema mixto, en base 5 y base 20, fue inventado en Mesoamérica, por los Mayas. En él, la unidad se representa por un punto, y cinco unidades en una barra horizontal. Las diferentes potencias de veinte se representan en posición vertical. Así, por ejemplo, los primeros números enteros, desde el cero hasta el diecinueve se representan de la siguiente manera

En El contador de arena, Arquímedes intenta establecer un límite superior para el número de granos de arena necesarios para llenar el universo. Para ello inventó los exponentes. Y nos proporcionó un ejemplo: el símbolo (10⁸)^ (10⁸ ^10⁸) representa un uno seguido de ochenta mil billones de ceros. Para sus propósitos, sin embargo, potencias mucho menores eran ya suficiente, pues según sus cálculos el universo debería tener un diámetro de 10¹⁴ estadios (2 años luz, aproximadamente) y por tanto podría llenarse con 10⁶³ granos de arena.

Mediante un proceso puramente sintáctico, en el que se manipulan ciegamente unos símbolos mientras se respetan unas determinadas leyes (la sintaxis propia de cada formalismo) podemos reproducir los razonamientos lógicos, como lo demostró por primera vez Aristóteles. Si yo afirmo, por ejemplo, “no es verdad que no es verdad que fui al cine”, podemos concluir sin mayor esfuerzo que en realidad sí fui al cine. Pero si afirmo que “no es verdad que no es verdad que no es verdad que no es verdad que no es verdad que fui al cine”, ya nos quedaría casi imposible saber si en realidad fuimos o no. El simbolismo del cálculo proposicional nos permite, sin embargo, conocer la respuesta: bastaría contar el número de negaciones de la proposición P, que representa la afirmación “fui al cine”. En la primera afirmación, por ejemplo, se afirma ┐┐P. Y como ┐┐P equivale a P, entonces concluimos que sí fuimos al cine. En el segundo ejemplo, se afirma ┐┐┐┐┐P que es equivalente a ┐P, y por tanto no fuimos al cine. La paridad del número de símbolos de negación “┐” nos permite entonces deducir la veracidad o falsedad de la correspondiente afirmación: si este número es par, es porque sí fuimos al cine; y concluimos que no fuimos, cuando dicho número es impar. La “máquina formal” calcula por nosotros la respuesta.

Hemos inventado muchos tipos de modelaciones, muchos tipos de formalismos, digámosles lenguajes: palabras, dibujos, croquis, mapas, diagramas, planos, partituras, ecuaciones, algoritmos. Entender es tener formalizada una serie de representaciones. Con estas podemos ir a la luna literalmente, podemos ir al principio y al fin del mundo, y al mismo tiempo saber que el “tiempo real” no existe, y solo existe como línea de mundo en el bloque intemporal de la 4-variedad que modela el universo einsteniano.

Gracias a los matemáticos y a sus garabatos en la mente y en la pizarra hemos podido comprender las leyes que gobiernan el mundo. Las teorías son representaciones que tienen una relación coherente con lo que somos capaces de observar de la realidad.

Como anotó mi padre, Antonio Vélez, en su artículo Modelación matemática: “La meta de la modelación es construir representaciones que sean físicamente isomorfas. Esto significa que por cada elemento relevante de la parte del mundo en estudio debe existir su correspondiente elemento en el modelo, y por cada ley o regularidad observada, otra en el modelo que la imite con cierta fidelidad. Son imitaciones osadas, que solemos llamar teorías. Máquinas virtuales en las que sus elementos son símbolos, llamados variables, parámetros, constantes, funciones, derivadas… Así, una longitud se puede remplazar por una letra; una velocidad o un gradiente, por una derivada o por un vector; un sistema económico, por una matriz; una estructura arborescente, por un fractal o por una ecuación de recurrencia; un trabajo realizado o una probabilidad, por una integral; el flujo de calor, por una ecuación en derivadas parciales; las impedancias, corrientes y voltajes en circuitos de corriente alterna, por números complejos… Al modelar, escogemos aquellos elementos matemáticos que mejor copien o simulen las propiedades pertinentes de la parcela del mundo que hemos elegido, sus invariantes.”

Es en el mundo de los símbolos y las ecuaciones matemáticas donde es posible explicar el movimiento planetario. En ese formalismo podemos comprender las dimensiones del Sol y de la Luna, y sus distancias relativas. ¡Inclusive podemos pesarlos!

Fue en un formalismo matemático donde por primera vez aparecieron unas sumas infinitas de funciones sinusoidales que representaban soluciones insospechadas de las ecuaciones de Maxwell. Después se supo que correspondían a las ondas electromagnéticas, esos objetos que todos habíamos percibido en forma de luz, y que nunca supimos qué eran.

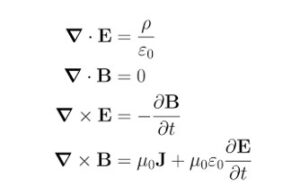
Y este descubrimiento que hizo posible la comunicación inalámbrica nació de la mente de un hombre “poco pragmático” cuyo interés se concentraba en asuntos tan poco terrenales como descifrar de qué estaban hechos “los anillos de Saturno”, o saber cómo establecer un lenguaje matemático elegante donde se pudiera escribir, y deducir de principios mínimos, las leyes empíricas de Ampere y Faraday.

Y de las ecuaciones de Einstein se sigue como corolario la existencia de agujeros negros, lugares imposibles del universo donde no existe la menor traza de materia, pero donde alguna vez hubo una estrella masiva, ahora convertida en un punto matemático sin dimensiones, ¡pero con su misma masa! Y la existencia de ondas de gravitación, que el mismo Einstein predijo, pero que solo hace un par de años pudieron finalmente observarse.

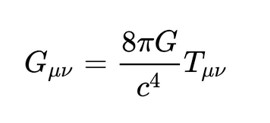
Y también se deduce la equivalencia entre masa y energía, la formula más famosa de toda la física, E=mc², de la cual se sigue la posibilidad de construir el arma definitiva capaz de destruir la civilización humana en su conjunto.

Y en el lenguaje inventado para representar la imposible raíz cuadrada de -1 se escribe la ecuación de Schrödinger, y la de Dirac, que nos muestra la realidad del misterioso mundo cuántico, y la existencia del positrón y de la antimateria.

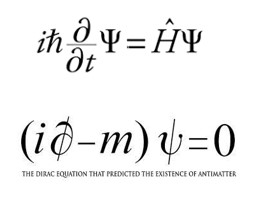
Y con ese otro lenguaje, que es la poesía, Borges se encuentra, y nosotros nos sincronizamos con él al decir:

«Negar la sucesión temporal, negar el yo, negar el universo astronómico, son desesperaciones aparentes y consuelos secretos. Nuestro destino (a diferencia del infierno de Swedenborg y del infierno de la mitología tibetana) no es espantoso por irreal; es espantoso porque es irreversible y de hierro. El tiempo es la sustancia de que estoy hecho. El tiempo es un río que me arrebata, pero yo soy el río; es un tigre que me destroza, pero yo soy el tigre; es un fuego que me consume, pero yo soy el fuego. El mundo, desgraciadamente, es real; yo, desgraciadamente, soy Borges».

Mi hermano es algebrista, y ha corregido y ampliado la información matemática de este artículo.