Las matemáticas de la cría de conejos

En la Edad Media surgen las primeras universidades y sus puertas son las primeras en abrirse a la física y a la matemática árabe y griega, recogiendo e incorporandosus grandes avances para entender problemas y fenómenos de la naturaleza que eran hasta entonces abordados sin explicación alguna o con solo aproximaciones adivinatorias o que se aceptaban como el azar en el juego de dioses juguetones o como artimañas de otros dioses arbitrarios, castigadores y condenatorios.

El surgimiento de las universidades aparece acompañado también del florecimiento de los retos para explicar la realidad desde el raciocinio. Y para resolver tales retos de la lejana Edad Media hubo personajes brillantes que hicieron grandes contribuciones, algunas de las cuales siguen encontrando, siglos después, aplicaciones insospechadas en áreas de reciente surgimiento. A uno de esos grandes personajes de la historia, no tan ampliamente conocido, me quiero referir en este artículo.

El matemático italiano Leonardo de Pisa (1175-1242), más conocido como Fibonacci (hijo de Bonacci), recopiló y difundió en Europa las enseñanzas árabes sobre la aritmética y el álgebra y se encargó además de mostrar la utilidad práctica del sistema de numeración indo-arábigo frente a la numeración romana. Podríamos por lo tanto responsabilizarlo de la numeración que hoy usamos, extendida desde entonces en Occidente. 

Pero su aporte fue mucho más que eso: en 1202 escribió un texto de Aritmética, Liber Abbacci “Libro del Ábaco” (también llamado “El Libro del Cálculo”) explicando a la audiencia europea avances árabes logrados a través de ingeniosos métodos y algoritmos. Incluyó criterios de divisibilidad, números primos y un compendio de los principales cálculos comerciales de contabilidad, pesos y medidas, destacando siempre las ventajas del uso del sistema de numeración arábigo. 

Otras de las obras más importantes de Fibonacci son: Practicae Geometricae, escrita en 1220 en la que reunió también principios de la trigonometría; de esta misma época es su manuscrito Flos (Ramillete de Soluciones de Ciertas Cuestiones Relativas al Número y a la Geometría) en el que desarrolla 15 problemas de ecuaciones diofánticas; es decir con coeficientes enteros para las que se buscan también números enteros como soluciones.

En el año 1225 Fibonacci hizo público (en la época no existía la imprenta) su cuarto libro Liber Quadratorum (El Libro de los Números Cuadrados): esta obra dedicada al emperador Federico II consta de veinte proposiciones originadas en los desafíos que le propuso Teodoro de Antioquía, matemático de la corte de Federico. Curiosamente, el año de publicación del libro es un número cuadrado.

Aun cuando el cuarto libro de Fibonacci es el más impresionante de su obra por sus aportes al examen y la construcción inductiva de métodos usados en lo que hoy conocemos como Teoría de Números, su fama no proviene de este trabajo sino de un problema de la tercera sección del  Liber Abbacci que condujo a la introducción de una sucesión cuyos términos son denominados los números de Fibonacci, desde cuando François Édouard Anatole Lucas estudió y escribió en 1877 sobre esta secuencia. 

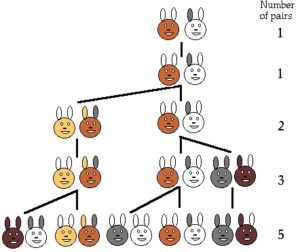
Esta sucesión fue descrita por Fibonacci como la solución a un problema de cría de conejos: se tiene una pareja de conejos en un lugar cerrado y se desea saber cuántos nacen a partir de esta pareja en un año, sabiendo que de acuerdo a su naturaleza cada pareja necesita un mes para ser adulta y cada pareja adulta necesita un mes más para procrear otra pareja. La respuesta a esta pregunta la deduce Fibonacci así: tenemos una pareja de conejos el primer mes. El segundo mes, la pareja envejece (todavía no procrea). El tercer mes, la pareja procrea otra pareja, o sea que ya tenemos dos. El cuarto mes, la pareja más vieja vuelve a procrear, mientras que la segunda envejece. En total, tenemos 3 parejas. El quinto mes, las dos parejas más viejas procrean de nuevo, y la tercera envejece; en total tenemos 3+2=5. El sexto mes, las tres parejas más viejas procrean, y las dos más jóvenes envejecen, de manera que tenemos 5+3 = 8 y así sucesivamente, de tal manera que obtenemos estos primeros números de parejas de conejos: 1, 1, 2, 3, 5, 8. Esta secuencia, en la que cada número es la suma de los dos números precedentes, extendida sin límite, es la que define la sucesión de Fibonacci que suele comenzarse con los números 0 y 1 (la regla de formación también funciona porque 0 + 1 = 1). Los números de fibonacci son entonces:  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,…

La fascinación por los infinitos números de Fibonacci obedece a múltiples aplicaciones que han venido descubriéndose, como es su utilidad para el tratamiento de mercados financieros, por ejemplo, pero también sus bellas interpretaciones gráficas, como es la conocida “Espiral de Fibonacci” y muy especialmente su conexión fundamental con el numero áureo o número de oro Φ, frecuentemente denominado como la divina proporción: es el valor numérico de la proporción que guardan entre sí dos segmentos cualesquiera de recta a y b (a más largo que b) donde a es al segmento b, como la longitud total (a+b) es al segmento a. El resultado es

(1+√5)/2 = 1.6180339887498948… 

La relación de los números de Fibonacci con el número áureo Φ ocurre porque la razón  entre un término de Fibonacci y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo; es decir que el límite cuando n tiende a infinito del cociente entre el término n-ésimo y el anterior de la sucesión de Fibonacci es precisamente el número Φ.

Entre las numerosas propiedades del número áureo (que daría para dedicar un artículo completo) destaco que curiosamente el propio número, su cuadrado y su inverso tienen las mismas cifras decimales. En efecto:

Φ = 1.6180339887498948… 

Φ² = 2.6180339887498948…

1/Φ = 0.6180339887498948…

En la obra de Leonardo Da Vinci llamada  El Hombre de Vitruvio, dibujo que se ha convertido en una de sus grandes creaciones, realizado por la época del descubrimiento de América, encontrado en uno de sus tantos diarios acompañado de notas anatómicas, Da Vinci representa una figura masculina desnuda en dos posiciones sobreimpresas de brazos y piernas e inscrita en un círculo y un cuadrado. Pues bien, en este dibujo, también conocido como “El Canon de las Proporciones Humanas”, Da Vinci logra plasmar las perfectas proporciones del cuerpo humano que fueron los resultados de los estudios que realizó a partir de los textos del arquitecto de la antigua Roma, Marco Vitrubio. El lado del cuadrado que enmarca la figura humana y el radio del círculo centrado en su ombligo tienen una relación que sorprendentemente también resulta ser precisamente la razón áurea Φ.

Fibonacci es el autor de otros resultados curiosos que no son muy conocidos o que han sido ignorados, pero que resultan absolutamente admirables. Por ejemplo, en 1225 es retado por Johannes de Palermo para que resuelva un problema que había sido planteado por el matemático árabe Omar Ibrahim Jayyam y calificado como muy difícil: encontrar una raíz del polinomio p(x) = x³+2x²+10x-20. Fibonacci prueba que ninguna de sus raíces es un entero ni una fracción ni la raíz cuadrada de una fracción. Demuestra que tiene una única raíz real, que está entre 1 y 2, y da una solución aproximada x = 1.368808107, correcta con nueve cifras decimales. Sin duda, este es un logro sorprendente para la época. Acostumbro dar este ejemplo a mis estudiantes cuando aprenden a programar métodos numéricos como el de Newton-Raphson para buscar ceros de funciones en forma aproximada y los reto a mejorar esta aproximación porque, aunque hoy usamos potentes computadores, esta tarea muestra a un Fibonacci grande, que logró hacerlo quizá ensayando el ábaco de origen oriental recién descubierto en occidente para su época.

@MantillaIgnacio