Las matemáticas detrás de un truco de magia.

Se ha hecho viral por estos días, otra vez, uno de esos vídeos que son presentados como descubrimientos asombrosos que desafían los más antiguos teoremas de la geometría plana, demostrados desde los griegos. Se trata de un vídeo (ese sí probablemente nuevo) en el que se presenta un viejo truco de magia que encaja dentro de un grupo de aparentes paradojas muy conocidas que aparecen al descomponer una figura plana en figuras geométricas y volverla a componer, obteniendo una superficie menor (o mayor) que la original.

Pero estas ilusiones geométricas que se acostumbran divulgar, especialmente a través de vídeos, recortando figuras planas y reconstruyéndolas de otra forma, esconden errores tan sutiles que se convierten en excelentes instrumentos para atraer a los niños a estudiar principios y propiedades matemáticas con el interés natural que despierta la curiosidad por descubrir la verdad.

Para ilustrar a los lectores sobre el tema, les invito a observar el siguiente vídeo, de los mejores que he visto, con ilusiones ópticas similares, publicado hace ya siete años y que ha tenido más de 9 millones de reproducciones: https://youtu.be/3PszMaZ5Ipk.

Aun cuando este tipo de exhibiciones apoyadas en aparentes paradojas geométricas se conocen desde el siglo XVI y hasta el propio Galileo Galilei usa este “método de disección” para concluir su famosa paradoja según la cual un punto podría tener la misma área que una circunferencia, es en 1953 cuando el mago de Nueva York, Paul Curry, crea un rompecabezas con solo cuatro piezas de madera para incluir, como un acto de magia, la ilusión de un cuadrado perdido. 

El truco de Curry es el mismo que utiliza “la magia” del video antes citado y voy a apoyarme en él para ofrecer una explicación. 

Se fabrica un rompecabezas con solo cuatro figuras para construir un triángulo rectángulo y se arma de dos formas distintas, mostrando que el triángulo resultante tiene áreas diferentes en cada caso, como indica la imagen: 

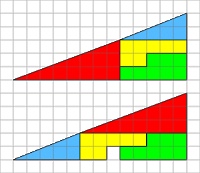
Como se observa, en efecto parece que el triángulo inferior tiene un área menor, pues faltaría el área del pequeño cuadrado perdido. Pero veamos cómo se justifica este “fenómeno”:

Usemos como unidades para el área los cuadraditos, como el faltante.

La pieza amarilla tiene un área de 7 cuadraditos.

La pieza verde tiene un área de 8 unidades.

La pieza roja es un triángulo rectángulo que tiene de base 8 cuadraditos y de altura 3 por lo tanto su área es de (8×3)/2 = 12 unidades.

La pieza azul es también un triángulo rectángulo de base 5 y altura 2, por lo tanto tiene un área de (5×2)/2 = 5 cuadraditos.

La suma de las áreas de las cuatro piezas es entonces:

7+8+12+5 = 32 unidades.

Sin embargo, la primera figura armada es un triángulo rectángulo que tiene de base 13 unidades y de altura 5. Por lo tanto su área sería:

(13×5)/2 = 32,5.

En la segunda figura hay que descontar una unidad correspondiente al cuadradito que falta, por lo tanto su área sería de 31,5 unidades; una menos que la primera figura.

¿Por qué?

La explicación es que la figura presentada como un triángulo formado por las cuatro piezas no es en realidad un triángulo, sino una figura de cuatro lados. En efecto: en el triángulo rojo el cateto opuesto al ángulo más pequeño es su altura, o sea 3 y el cateto adyacente es su base, igual a 8 cuadraditos, por lo tanto la tangente de ese ángulo es 3/8; lo que quiere decir que corresponde a un ángulo de 0,35877067 radianes; es decir unos 20,5560 grados.

En la primera figura armada el mismo ángulo tiene como cateto opuesto 5 unidades y como cateto adyacente 13. Entonces la tangente del ángulo es 5/13, o sea que el ángulo es de o,36717383 radianes o, lo que es lo mismo, 21,0375 grados.

Como se observa, al corresponder estos valores, en ambos casos, al mismo ángulo (el más pequeño del triángulo rojo), debería obtenerse el mismo valor, pero no son iguales como debería ocurrir si la figura armada fuese un verdadero triángulo; hay una diferencia cercana a medio grado, más exactamente de 0,4815 grados. La primera figura tiene una “hipotenusa convexa” compuesta de dos rectas que aumentan el área del verdadero triángulo y la segunda figura tiene una “hipotenusa cóncava” que disminuye el área del verdadero triángulo, produciendo el efecto buscado.

Naturalmente nuestra capacidad visual no puede descubrir esa pequeña diferencia y esta limitación produce la ilusión óptica que nos hace creer que se trata de un acto de magia, reforzado aún más con la diferencia que se produce en el área total de la figura armada, igual a una unidad, que corresponde al cuadradito adicional.

Espero haber logrado distraerles con la magia de las matemáticas para descubrir un bonito truco mágico; y en estos días de aislamiento puede aprovecharse para realizarlo en casa, con los niños, utilizando una barra de chocolate, de las que vienen en cuadritos. Solo hay que saberla partir muy bien para poderles ganar un cuadrito de chocolatina a los pequeños.

@MantillaIgnacio