La paradoja de Zenón

Zenón de Elea fue un filósofo griego que vivió en el siglo V a.C. Nació, como su maestro Parménides, en la antigua ciudad griega de Elea, situada en la costa sudoccidental de la península itálica, cerca de la actual ciudad de Salerno. Escribió un libro sobre la naturaleza, orientado a defender las tesis de Parménides usando principalmente razonamientos que, según Aristóteles, producen dolor de cabeza. 

Zenón fue el inventor del razonamiento paradójico y en lugar de demostrar las tesis de Parménides, lograba debilitar las de los detractores con conclusiones que eran más aceptables que las de ellos. Fue así como logró plantear unas 40 paradojas dedicadas principalmente a demostrar las inconsistencias de los conceptos de espacio, tiempo, movimiento y pluralidad en la noción del continuo. Dentro de las paradojas más famosas formuladas por Zenón hay una, difícil de rebatir, que se conoce como la paradoja del corredor, según la cual un corredor nunca alcanza su meta.

El enunciado de esta paradoja es como sigue: «un corredor no puede alcanzar nunca la meta porque siempre ha de recorrer la mitad de una distancia antes de recorrer la distancia total. Es decir, cuando haya recorrido la primera mitad, tendrá que recorrer la otra mitad. Cuando haya recorrido la mitad de ésta, le quedará todavía la cuarta parte y así sucesiva e indefinidamente».

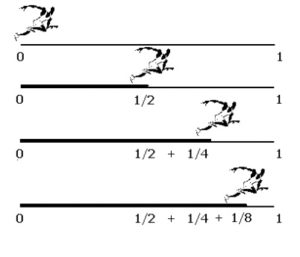
En realidad, la afirmación de Zenón dio lugar a un largo debate que ocupó a muchos filósofos y matemáticos durante siglos, intentando explicar la creencia según la cual un número infinito de cantidades positivas no podía tener una suma finita. Este asunto tardó 2000 años para ser rebatido, entendido y formulado con toda precisión gracias al cálculo infinitesimal y más exactamente a la teoría de las series infinitas.  

Para los lectores interesados, esta paradoja se puede rebatir formalmente como aparece al final, donde reproduzco una pieza maestra del análisis matemático, demostrando que si el corredor, trotando a velocidad constante, tarda un tiempo t en recorrer la mitad de la distancia, debe tardar el doble del tiempo, es decir 2t, en recorrer la distancia total. (*)

La paradoja de Zenón encierra una idea muy interesante, que se precisa muy bien con la teoría de las series infinitas haciendo una distinción entre series tales como la serie armónica

que diverge y una serie como la que describe la paradoja de Zenón, que sí es convergente.

Las series infinitas divergentes no se pueden operar con las leyes usuales del álgebra como si fueran sumas ordinarias finitas, pues es posible que conduzcan a resultados incorrectos que aparentemente no esconden error alguno. Por ejemplo, la serie:

1-1+1-1+1-1+- ··· 

si se opera asociando

(1-1)+(1-1)+(1-1)+- ··· = 0+0+0+ ··· = 0;

pero si se asocia como

1+[-1+1-1+1-1+- ···] = 1+[(-1+1)+(-1+1)+(-1+1)+ ···] = 1+0+0+0+ ··· = 1.

Esto significa que la ley asociativa para la suma no se cumple cuando se trata de una suma infinita divergente.

(*) Una demostración

Naturalmente si se quiere rebatir la paradoja, lo interesante es hacerlo respetando la partición que hace Zenón donde cada fracción es la mitad de la anterior y calcular los tiempos parciales que va necesitando el corredor para recorrer las distintas fracciones de la carrera hasta la meta.

Los tiempos parciales que necesita el corredor son:

p(1) = t

para alcanzar la mitad (1/2) del recorrido. Como necesita la mitad de ese tiempo para recorrer ahora la cuarta parte, entonces

p(2) = t + t/2 = 3t/2

es el tiempo acumulado necesario para avanzar hasta el siguiente punto que corresponde a

1/2 + 1/4 = 3/4

del recorrido. En la siguiente fracción de la carrera tenemos que

p(3) = t + t/2 + t/4 = 7t/4

es el tiempo acumulado necesario para avanzar al siguiente punto o sea

1/2 + 1/4 + 1/8 = 7/8

del recorrido. Y continuando con este análisis tenemos que

p(4) = t + t/2 + t/4 + t/8 = 15t/8

es el acumulado para avanzar la mitad del recorrido anterior y llegar al punto

1/2 + 1/4 + 1/8 + 1/16 = 15/16

del recorrido total.

Y en general, para alcanzar el punto

1/2 + 1/4 + 1/8 + 1/16 + … + 1/(2^n+1)

del recorrido, habrá acumulado un tiempo de

p(n+1) = t + t/2 + t/4 + t/8 + … + t/(2^n).

Si nos concentramos en los tiempos utilizados, observamos que:

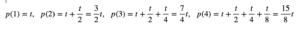
y estos tiempos se pueden escribir como:

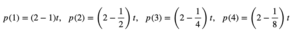
de donde se deduce la fórmula general para el tiempo acumulado por el corredor:

  para todo n natural.

Ahora bien, es evidente que la sucesión {P(n)} tiende a 2t cuando n tiende a infinito, pero como lo observamos antes, esta sucesión es en realidad la sucesión de sumas parciales de la serie

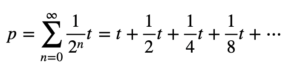
por lo tanto

Entonces el corredor de la paradoja de Zenón sí alcanza la meta y lo hace en el doble del tiempo que necesita para recorrer la mitad de la distancia total.

@MantillaIgnacio