El juego del 15

La clasificación de los números naturales entre pares e impares tiene una especial  importancia para las permutaciones; es decir, para los distintos arreglos o reordenamientos que pueden lograrse con una lista de objetos. Si nos limitamos a los números como objetos, se puede entender fácilmente el concepto de permutación con una sencilla ilustración; así por ejemplo, las permutaciones de la lista 1, 2, 3 son seis en total:

123, 132, 213, 231, 312, 321.

Cuando la lista contiene n objetos, el número total de permutaciones posibles es:

n! = n•(n-1)•(n-2)•…•2•1

porque podemos elegir el primer elemento de n maneras, el segundo de n-1, el tercero de n-2 y así sucesivamente hasta el último. Por lo tanto si vamos a permutar los objetos de una lista de 4 objetos, tenemos 4! = 4•3•2•1 = 24 formas de hacerlo.

A una permutación de n objetos se le asocia una paridad, es decir, la permutación puede ser par o impar. Cuando n ≥ 2, hay exactamente n!/2 permutaciones pares y n!/2 permutaciones impares. El caso n = 1 no es interesante, pero (para los puristas) en este caso hay solo una permutación par y ninguna impar.

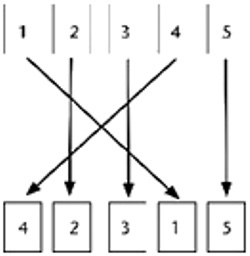
Hay una manera sencilla de calcular la paridad de una permutación de n objetos cuando n no es muy grande, como es el caso que vamos a considerar después; basta escribir en orden la lista con los números de 1 a n en una fila y la lista con la permutación de esos números en otra, que puede estar debajo. Luego se unen los números iguales de ambas listas mediante una línea, evitando que tres o más líneas se crucen en un mismo punto o que una misma línea (que puede ser curva) se cruce a sí misma. Después se cuenta el número de intersecciones de las líneas. Si el número de intersecciones es par, la permutación también lo es y si es impar, la permutación es impar. Así por ejemplo, la permutación 42315 de 12345 es impar porque se pueden contar exactamente 5 intersecciones.

Una bonita aplicación de este concepto de paridad es la que tiene en el popular juego del 15, también conocido como cuadrado o rompecabezas del 15, fabricado por primera vez en Estados Unidos por el empresario Matthias Rice a finales de 1879. En 1880, el odontólogo Charles Pevey ofreció un premio y una dentadura postiza a quien consiguiera dar con una secuencia que nadie logró.

El juego, de tipo solitario, consiste en un cuadrado de 4×4 en donde están ubicadas 15 fichas corredizas de 1×1 numeradas del 1 al 15 y un cuadro vacío del mismo tamaño de las fichas. Solo una ficha adyacente al cuadro vacío puede moverse hasta él y deja vacío el cuadro que ocupaba. El objetivo del juego es lograr ordenar las fichas desde la número 1 hasta la número 15; aunque se pueden intentar otras secuencias.

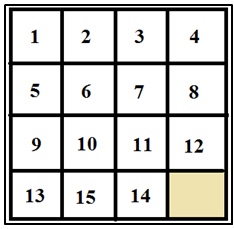
El interés en este rompecabezas fue reavivado en 1886 por el autor de Puzzles Sam Loyd, al ofrecer un jugoso premio de 1000 dólares a quienes resolvieran el problema de ordenar las fichas del 1 al 15, de menor a mayor, partiendo de una permutación que solamente se diferenciaba de la disposición ordenada, por la inversión de los números 14 y 15 como muestra la figura:

Loyd estaba seguro de que nadie ganaría el premio, pues sabía que ese problema no tiene solución. En efecto, veamos por qué es imposible dar con la solución.

Cualquier posición en el juego puede interpretarse como una permutación de la posición original, usando la casilla vacía como si fuese la pieza 16. Con estas consideraciones hay que pasar, con los movimientos permitidos, de una permutación impar como es la que se obtiene de intercambiar la casilla 14 con la 15, es decir:

(1,2,3,4,5,6,7,8,9,10,11,12,13,15,14,16) 

a otra que es par, como es la que debe conseguirse al final:

(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16).

Pero cuando hacemos un movimiento permitido tenemos dos posibilidades: hacer un desplazamiento horizontal o uno vertical. Los movimientos horizontales no modifican la permutación y solo mueven la casilla vacía en la misma fila, pero en cambio si movemos una ficha hacia abajo, el número correspondiente sobrepasa a los tres que tiene adelante y la casilla vacía, que estaba debajo, pasa a ocupar la posición que tenía la ficha que se movió, por lo tanto el número de intersecciones de las líneas que unen la permutación anterior con la nueva (como se explicó arriba) debe ahora diferir en 3, entonces la permutación resultante tiene paridad diferente a la permutación de partida. De modo análogo, si hacemos un movimiento permitido, verticalmente hacia arriba, la casilla vacía cambia de fila y la paridad de la permutación resultante cambia.  

En el reto, el requisito de que la casilla 16 (la vacía) deba terminar en la misma posición inicial implica que el número de los movimientos verticales válidos realizados debe ser par, porque la casilla vacía debe haber subido y bajado las mismas veces, por lo tanto la paridad de la permutación tendría que cambiar un número par de veces y cada vez con una diferencia de 3 intersecciones, lo que significa que al final tiene que quedar con la misma paridad inicial, o sea que la permutación final es impar. Entonces es imposible conseguir la permutación par

(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16) 

a partir de la permutación impar

(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16).

Recordemos que el número de permutaciones posibles con 16 elementos es igual a 

16! = 20.922.789.888.000, 

de las cuales la mitad corresponde a permutaciones pares y la otra mitad a impares. Así que en este reto se podría llegar a un total de

16!/2 = 10.461.394.944.000

posibles reordenamientos.

Acudiendo al ensayo y error, y suponiendo que una persona realiza un movimiento cada 5 segundos, tendríamos 12 movimientos por minuto, o sea 720 en una hora, 17.280 diarios, por lo tanto se requerirían más de 600 millones de días que son más de un millón y medio de años para poder explorar todos los reordenamientos posibles. Esto fue un estímulo entre la gente que, con frenesí, creía que había que seguir intentándolo para dar con una solución inexistente y cobrar el premio.

El juego del 15 es un entretenido pasatiempos, muy económico, que bien puede aliviar el confinamiento por estos días. Ojalá lo disfruten, pero antes de intentar una secuencia en particular hay que verificar, como se hace en matemáticas, que la solución existe.

@MantillaIgnacio