Al rescate de la geometría

Para muchas personas las matemáticas de la secundaria fueron aburridas o tortuosas, razón por la que no quisieron elegir carreras con un mediano componente matemático. Se cree que una buena parte de esta percepción sobre las matemáticas aprendidas con disgusto o no aprendidas en el colegio ha sido responsabilidad de los docentes de matemáticas, pero la verdad es que también han influido los programas elaborados desde el Ministerio de Educación que en las últimas décadas se ha encargado de ir eliminando contenidos que hacían las clases fascinantes. 

Se han suprimido conceptos muy útiles y formativos que anteriormente eran de obligatorio aprendizaje y se han distribuidos algunos tópicos en varios grados que aparentemente abarcan más temas; pero al final solo aportan un mar de conocimientos con un centímetro de profundidad.

Me refiero especialmente a los capítulos dedicados a la Geometría Euclidiana, esa que se estudiaba con rigor, como asignatura independiente, cuyo texto guía por muchos años en toda Hispanoamérica fue el libro de Geometría de G. M. Bruño, publicado a comienzos del siglo pasado y que hoy puede descargarse en PDF de manera gratuita. Sí, me refiero a esa geometría que se aprendía usando como herramientas el lápiz, el cuaderno cuadriculado, el borrador, la escuadra, el transportador, la regla, el compás y que, usando tizas de colores, los docentes se esforzaban por explicar con trazos rectos y círculos perfectos en el tablero que luego producía lástima tener que borrarlo.  

No pretendo que volvamos a esas herramientas solamente, aunque no comparto la idea de jubilar la escritura a mano; no hay duda de que hoy las gráficas pueden ser computarizadas y con programas como “Geogebra” es fácil mejorar el entendimiento de la mayoría de los tópicos geométricos; también con la asistencia de la Inteligencia Artificial puede facilitarse hoy su comprensión, pero quiero llamar la atención sobre la necesidad de que al menos se les dé a conocer y se les permita disfrutar a los niños y jóvenes, de la Geometría Euclidiana en forma integral e independiente, sin prohibir las herramientas y ayudas modernas que quieran utilizar para que sea aún más atractiva para su propio deleite.  

Los conceptos, postulados, figuras, axiomas, teoremas, corolarios y demostraciones de la Geometría Euclidiana constituyen la mejor visión de las matemáticas. No debemos reemplazar tal riqueza con una dispersa y superficial noción en el bachillerato; es como vivir en el penthouse del piso 30 y cubrir las ventanas para ocultar la vista y evitar la luz. 

Los tópicos más conocidos de la Geometría Plana están contenidos en el famoso libro “Elementos”, que nos dejó el matemático griego Euclides, obra escrita hace más de 23 siglos, pero hay también resultados y aplicaciones que han sido descubiertos recientemente y que pueden incentivar a los jóvenes a cultivar el estudio de las matemáticas con nuevos retos, usando herramientas modernas. Menciono solo la abundante oferta de juegos electrónicos, que basan sus diseños y presentación en conceptos geométricos.

Después de Euclides y a lo largo del tiempo, desde la invención de la imprenta en 1450, han aparecido incontables ediciones del trabajo de Euclides, como esta bella publicación:

que usa para las demostraciones solamente ilustraciones como estas:

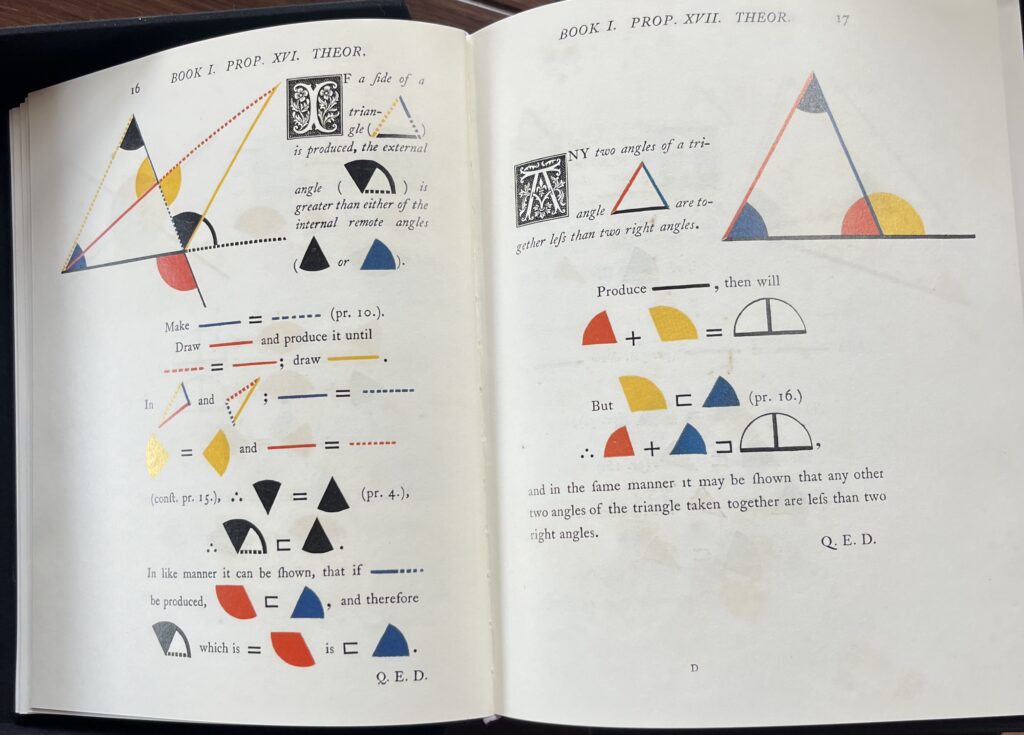
Tampoco la investigación y los resultados en Geometría Euclidiana después de Euclides cesó; incluso el emperador Napoleón Bonaparte hizo un original aporte al formular y demostrar el conocido “Teorema de Napoleón” sobre el que hace unos años escribí (ver: https://www.elespectador.com/opinion/columnistas/ignacio-mantilla/el-teorema-de-napoleon-column-729818)

Ahora bien, no podría cerrar este llamado para recuperar la enseñanza de la Geometría Euclidiana sin ofrecer al menos un buen ejemplo, como lo haré continuación. Pero antes un poco de contexto: comúnmente los matemáticos sentimos mayor aprecio por un teorema en particular en cada área estudiada, y ese teorema favorito lo podemos escribir y demostrar de memoria; así por ejemplo, en mi caso, el Teorema de Punto Fijo de Banach es mi favorito del Análisis Matemático y el Teorema de Infinitud de los Números Primos, demostrado por Euclides usando el método de reducción al absurdo, es mi favorito de la Teoría de Números. 

En el caso de la Geometría Euclidiana también tengo mi favorito, y no es el Teorema de Pitágoras, sino uno, bastante menos famoso y poco conocido. Se trata de un resultado de una extraordinaria sencillez que tiene múltiples aplicaciones, me refiero a un bonito resultado publicado hace 200 años, más exactamente en 1822, o sea después de 2000 años de Euclides, conocido como el “Teorema de Poncelet”, de autoría del matemático e ingeniero militar francés Jean-Victor Poncelet (1788-1867), quien estuvo en una prisión rusa entre 1812 y 1814 tras participar en la campaña napoleónica. De este período prolífico son sus trabajos publicados años después. El teorema mencionado es el siguiente:

Teorema de Poncelet

En un triángulo rectángulo la suma de los catetos a y b es igual a la suma de la hipotenusa c y el doble del radio R de la circunferencia inscrita. O sea:

a + b = c + 2R.

La demostración de este fascinante resultado es sencilla. Basta observar la siguiente figura en donde están presentes dos resultados que son conocidos:  

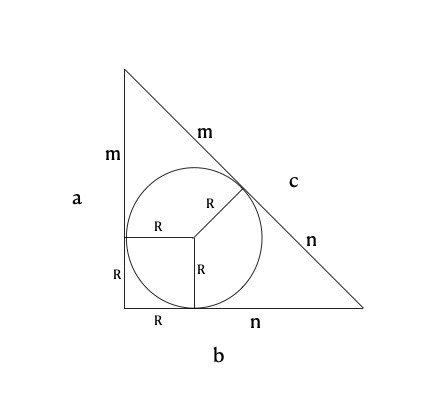
1. Los dos segmentos de rectas tangentes, trazados desde un mismo punto exterior a un círculo, tienen la misma longitud; por lo tanto los segmentos que unen los vértices de los ángulos no rectos del triángulo y los puntos de tangencia con la circunferencia son, en cada caso, de la misma longitud; es decir m en un caso y n en el otro. 
2. El cuadrilátero que forman los dos radios que unen el centro de la circunferencia con los puntos de tangencia en los catetos a y b del triángulo y los dos segmentos que desde estos puntos de tangencia unen el vérttice del ángulo recto del triángulo, es un cuadrado de lado R.

Ahora la demostración resulta trivial pues:

a + b = (m + R) + (R + n) 

         = m + n + 2R

         = c + 2R.

Una de las imágenes más bellas de la Geometría Euclidiana se obtiene usando precisamente el Teorema de Poncelet. En efecto: por el Teorema de Pitágoras se sabe que el triángulo de lados (3, 4, 5) es un triángulo rectángulo (3² + 4² = 5²); esta es la tripla pitagórica más conocida y lo que resulta alucinante es que el círculo que puede inscribirse en ese triángulo, tiene un área de π unidades cuadradas. La prueba de esta bella relación resulta inmediata usando el Teorema de Poncelet, porque: 

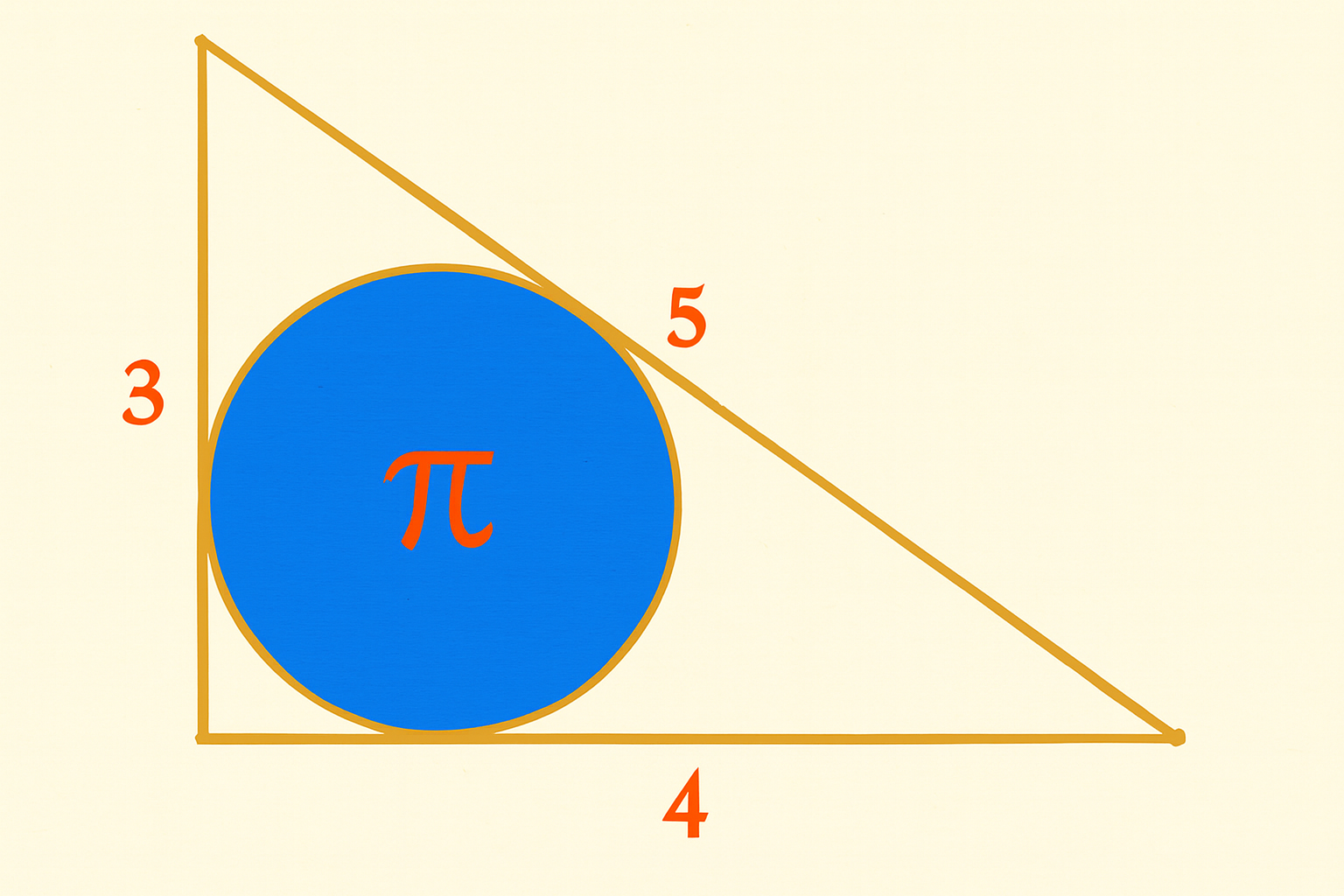
3 + 4 = 5 + 2R,

entonces el radio R del círculo debe ser R = 1, y reemplazando en la fórmula del área del círculo:

A = π·R² = π·1² = π.

¿No es esto sorprendente? Prácticamente puede definirse el número π como el área del círculo que puede inscribirse en la primera tripla pitagórica (3, 4, 5).

Así como se afirma que la ecuación más bella de las matemáticas es la Ecuación de Euler: 

Finalizo con una frase del matemático y astrónomo alemán Johannes Kepler (1571-1639): 

“Donde haya materia existe geometría”.

@MantillaIgnacio