Mental modeling or formalism: extraordinary creation of human culture

The brains of living organisms are essentially machines designed by evolution to represent external reality. They are the result of 4,000 million years of evolutionary pressure, which subjects all forms of life incessant struggle for survival, at every moment, in every environment,

At the dawn of life, the first brains were nothing more than small groups of neurons capable of interpreting the direction of a light source, and thus starting a flagellum that could guide its owner to the source of food, abundant in the surface of the primordial oceans. Those same structures, simple at first, became more intricate machines as primitive photoreceptors evolved into more and more complex eyes. The binary world of light and darkness gradually gave way to a universe of shapes, backgrounds, colors, textures… Each of the four dimensions, time and space, should have been represented in larger neural networks, in wiring of axons and dendrites that as a whole constitute an abstract, crude and poorly approximate internal representation of that elusive phantom that we call the “external world”.

In the words of neuroscientist Rodolfo Llinás, “We have eyes that evolved to generate images of the external world through the bouncing properties of photons. But what is an image? An image is a simplification of reality. The brain constantly simplifies reality; furthermore, it simplifies the external world, but in a very useful way. An image is a simplified representation of the external world written in a strange way. Any sensory transduction is a simplified representation of a universal emanating from the external world. The brain is very Kantian in terms of the essence of its operations”.

The brain, we still don’t know how it does it, presents to that ethereal and elusive object that we call “I” a representation (our “reality”) of the world in which we inhabit. However, in the human brain, and to a lesser extent in that of some other higher mammals, something unusual has happened: that same internal representation is expressed externally, a mechanism without which communication would be impossible. Language itself, as the great linguist Noam Chomsky points out, did not appear with grunts and guttural gestures, as some naively suppose, but was probably in its origins an extension of that internal “mentalese” that must have appeared first in the wire of the neural network to make the same reality compatible between members of the same species.

But language is not limited to our linguistic capacity. Symbols, such as words, can also be abstract objects, characters created to represent categories, relationships, order, functionality… It is these symbols that allow us to discover and invent new worlds, unreachable to our limited senses, no less real extensions of our perceptual world. Mathematicians call this tool formalisms and philosophers, mental modeling. All human civilization, to a large extent, is the product of that “magic” wand in the hands of everyone.

In his book, How We Discovered Numbers, the writer Isaac Asimov offers us a palpable example. How does one hunter tell another that he killed a bear twenty-five days ago if he does not know the concept of “whole number”? Such a person could use, as children do, the fingers of the hands to simulate twenty-five consecutive events. And the mechanism soon runs out without appropriate symbols as what happened becomes more and more remote. The use of pebbles and other objects provides a first resource.

Some animals, such as crows, can make abstract representations of the smallest integers (positive and negative). In a famous experiment, a man enters a wooden house that is right next to a small feeder for the animal. From a tree, the raven watches him. Only when the man comes out again does the bird get close to the food that is left there. Then two men enter, and only one leaves. The raven, who knows that two minus one is not zero, and does not come close to his food until the second man decides to leave. The experiment is repeated with six, seven and up to ten men who enter at the same time, and then leave in groups of two, of three… The crow secretly keeps the accounts: 10 minus 2, minus 3… Only if the account remains at zero the animal risks entering. Larger groups confuse it; the animal errs when its mental representation system exceeds its limited, although extraordinary arithmetic capacity.

Positional number systems are paradigmatic examples of the first mathematical formalisms. In the decimal system, to cite an example, we use the Arabic digits to represent the first integers up to nine (including zero, representing the void, nothing). Then, on the left, the new digit represents the number of powers of ten. The next one to the left represents the number of powers of one hundred, and so on. The advantages with respect to the Roman numeral system can be appreciated when it is necessary to do any moderately complex computation. For example, let’s try dividing MDXXXV by DLIX, using the Roman numeral system.

Another positional system was invented by the Babylonians: in base 60, it used bars for units and wedges for powers of 60. It’s amazing, it’s still used to divide the circle into 360 degrees.

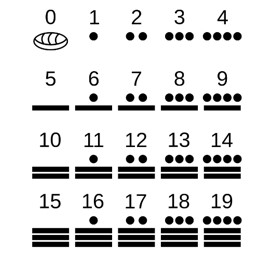
Another mixed system, based on 5 and base 20, was invented in Mesoamerica, by the Mayas. In it, the unit is represented by a point, and five units in a horizontal bar. The different powers of twenty are represented upright. Thus, for example, the first integers, from zero to nineteen are represented as follows:

1. In The Sand Counter, Archimedes tries to set an upper limit on the number of grains of sand needed to fill the universe. For this he invented the exponents. And he gave us an example: the symbol (108) ^ (108 ^ 108) represents a one followed by eighty thousand trillion zeros. For his purposes, however, much smaller powers were already sufficient, since according to his calculations the universe should have a diameter of 10¹⁴ stadia (approximately 2 light years) and therefore could be filled with 10⁶³ grains of sand.

Through a purely syntactic process, in which symbols are blindly manipulated while certain laws are respected (the syntax of each formalism), we can reproduce logical reasoning, as Aristotle first demonstrated. If I affirm, for example, “it is not true that it is not true that I went to the cinema”, we can easily conclude that I actually did go to the cinema. But if I affirm that “it is not true that it is not true that it is not true that it is not true that it is not true that I went to the cinema”, it would be almost impossible for us to know if we really went or not. The symbolism of the propositional calculus allows us, however, to know the answer: it would suffice to count the number of denials of the proposition P, which represents the affirmation “I went to the cinema”. In the first statement, for example, ┐┐P is stated, where ┐means not or negation. And since ┐┐P is equal to P, then we conclude that we did go to the movies. In the second example, it is stated that ┐┐┐┐┐P is equivalent to ┐P, and therefore we did not go to the cinema. The parity of the number of negation symbols “┐” then allows us to deduce the truth or falsity of the corresponding statement: if this number is even, it is because we did go to the movies; and we conclude that we did not go, when said number is odd. The “formal machine” calculates the answer for us.

We have invented many types of models, many types of formalisms, let’s say languages: words, drawings, sketches, maps, diagrams, plans, scores, equations, algorithms. To understand is to have formalized a series of representations. With these we can literally go to the moon, we can go to the beginning and the end of the world, and at the same time to know that “real time” does not exist, and only exists as a world line in the timeless block of the 4-manifold that models the Einsteinian universe.

Thanks to mathematicians and their doodles in the mind and on the blackboard, we have been able to understand the laws that govern the world. Theories are representations that have a coherent relationship with what we are able to observe of reality.

As my father, Antonio Vélez, noted in his article Mathematical Modeling: “The goal of modeling is to construct representations that are physically isomorphic. This means that for each relevant element of the part of the world under study there must be a corresponding element in the model, and for each law or regularity observed, another in the model that imitates it with some fidelity. They are bold imitations, which we usually call theories. Virtual machines in which their elements are symbols, called variables, parameters, constants, functions, derivatives… Thus, a length can be replaced by a letter; a velocity or a gradient, by a derivative or by a vector; an economic system, by a matrix; a tree structure, by a fractal or by a recurrence equation; a work done or a probability, by an integral; the heat flux, by an equation in partial derivatives; the impedances, currents and voltages in alternating current circuits, by complex numbers… When modeling, we choose those mathematical elements that best copy or simulate the pertinent properties of the parcel of the world we have chosen, its invariants.”

It is in the world of symbols and mathematical equations where it is possible to explain the planetary movement. In this formalism we can understand the dimensions of the Sun and the Moon, and their relative distances. We can even weigh them!

It was in a mathematical formalism where for the first time infinite sums of sinusoidal functions appeared that represented unsuspected solutions of Maxwell’s equations. Later it was learned that they corresponded to electromagnetic waves, those objects that we had all perceived in the form of light, and that we never knew what they were.

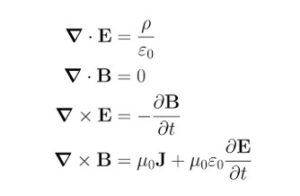
And this discovery that made wireless communication possible was born from the mind of a “not very pragmatic” man whose interest was concentrated in matters as unearthly as deciphering what “the rings of Saturn” were made of, or knowing how to establish an elegant mathematical language. where one could write, and deduce from minimal principles, the empirical laws of Ampere and Faraday.

And from Einstein’s equations it follows as a corollary the existence of black holes, impossible places in the universe where there is not the slightest trace of matter, but where once there was a massive star, now converted into a dimensionless mathematical point, but with its very mass! And the existence of gravitational waves, which Einstein himself predicted, but which could only be observed a couple of years ago.

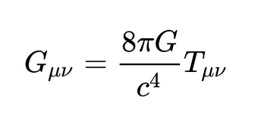
And the equivalence between mass and energy is also deduced, the most famous formula in all of physics, E=mc^2, from which follows the possibility of building the ultimate weapon capable of destroying human civilization as a whole.

And in the language invented to represent the impossible square root of -1, Schrödinger’s equation is written, and Dirac’s, which shows us the reality of the mysterious quantum world, and the existence of the positron and antimatter.

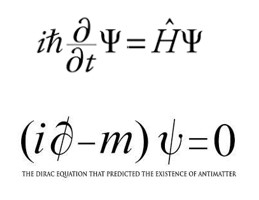
And with that other language, which is poetry, Borges meets, and we synchronize with him when saying:

“Time is the substance I am made of. Time is a river which sweeps me along, but I am the river; it is a tiger which destroys me, but I am the tiger; it is a fire which consumes me, but I am the fire.”

My brother expanded and corrected the mathematical information in this article.